My Notes

# PCA

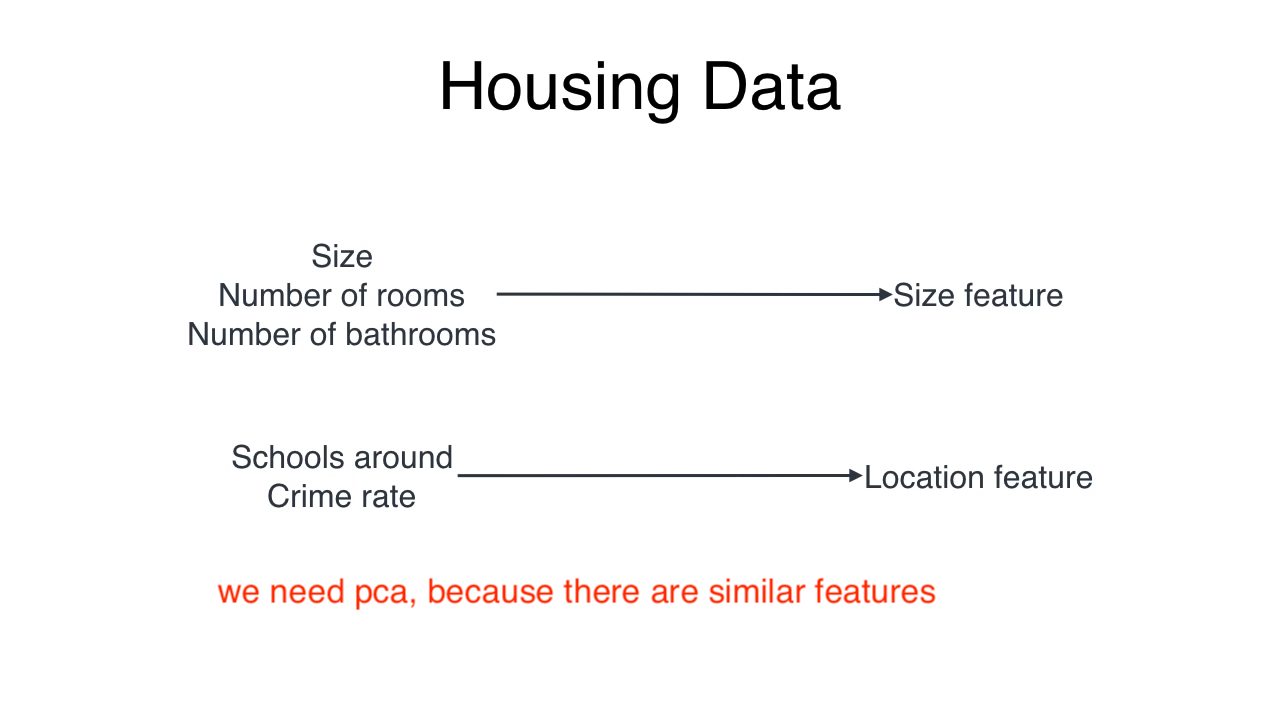
Latent Features

All those features describe the house. But they generally fall under 2 categories.

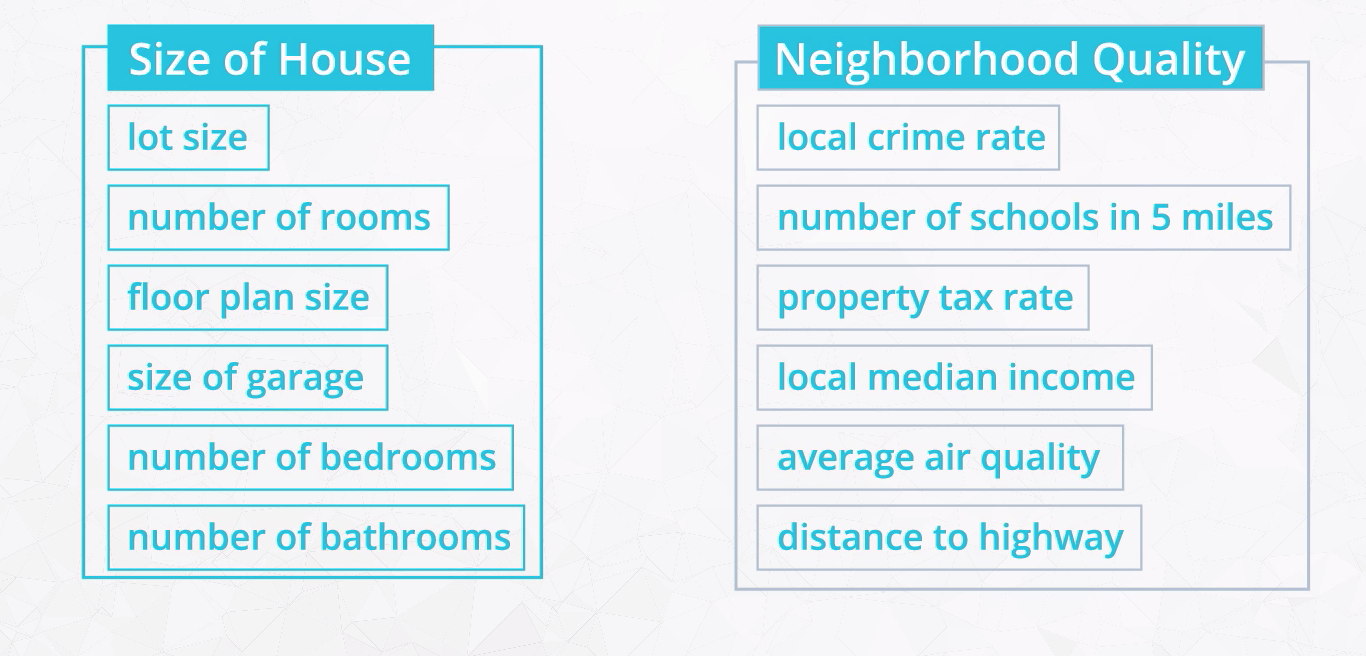
#How to select features

# Feature Selection

involves finding a subset of original features of your data

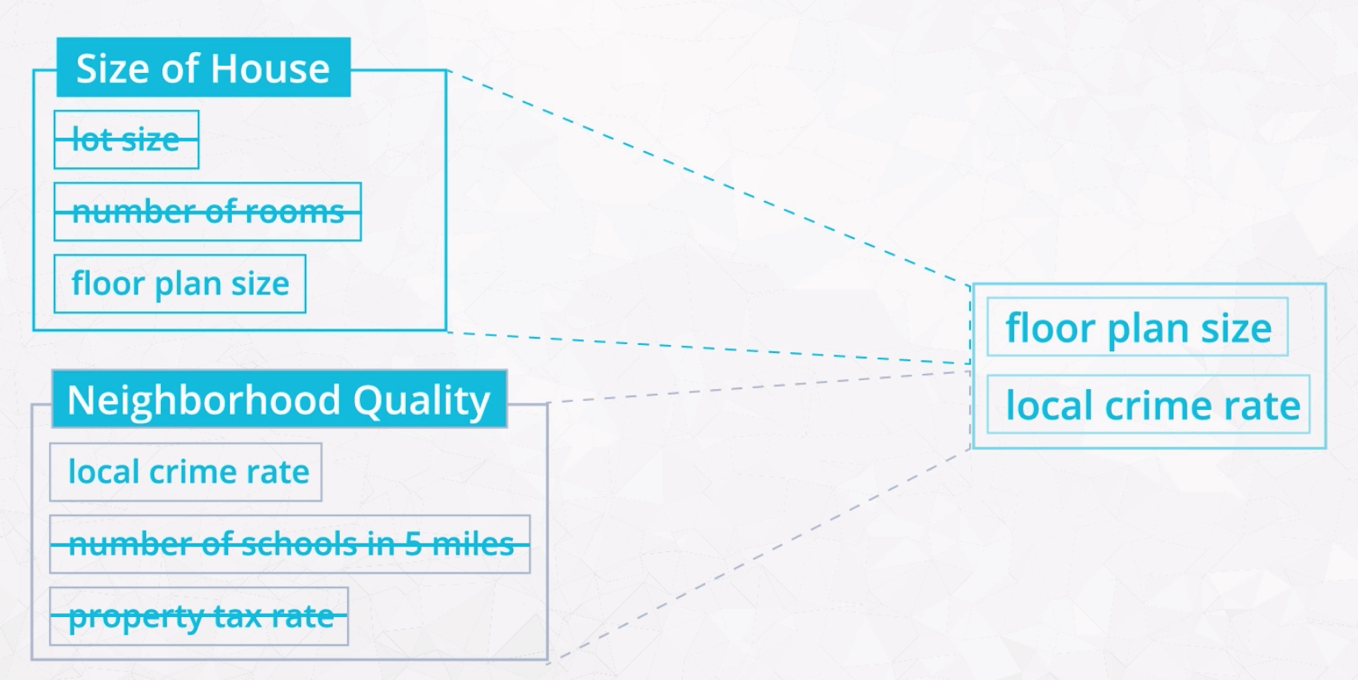
Methods: Filter Methods: use a ranking or sorting algorithm to select useful features. Some techniques are Pearson's Correlation, Linear Discriminant Analysis (LDA), and Analysis of Variance (ANOVA).

Wrapper Methods: Select features by directly testing performance on model. Common Examples of wrapper methods are Forward Search, Backward Search, and Recursive Feature Elimination.

# Feature Extraction

involves constructing new features called latent features

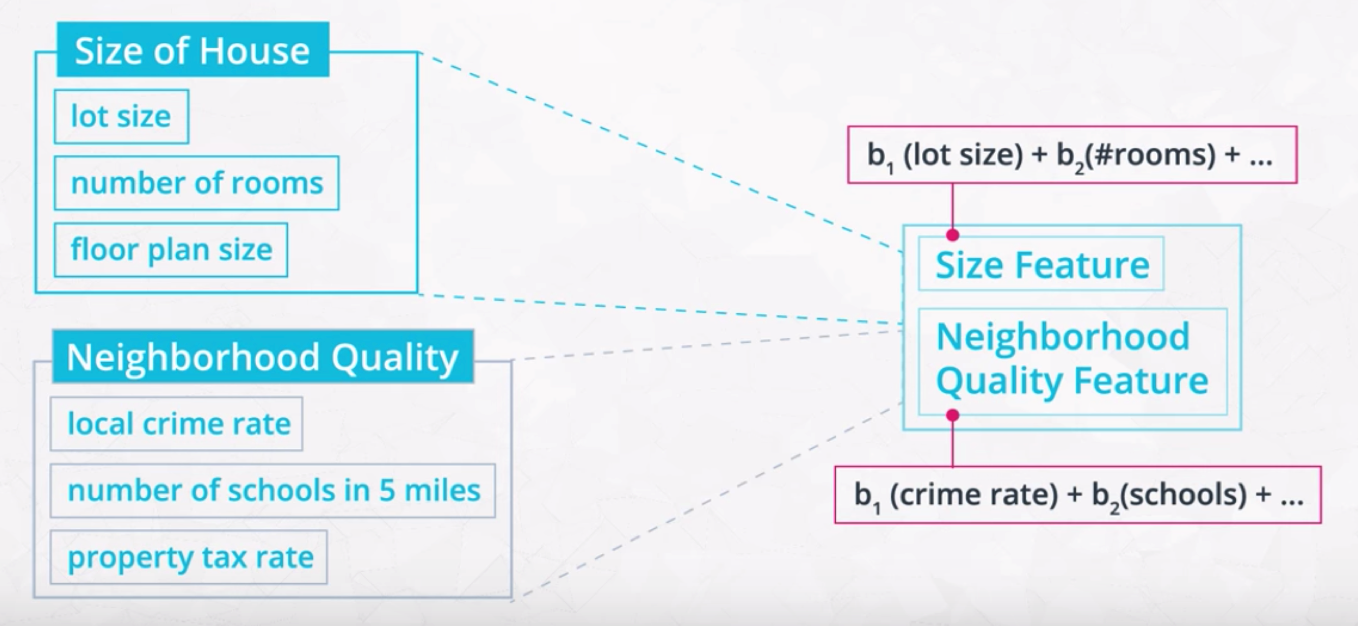
Techniques involded Principal Component Analysis, Independent Component Anlaysis , Random Projection.

Ref:

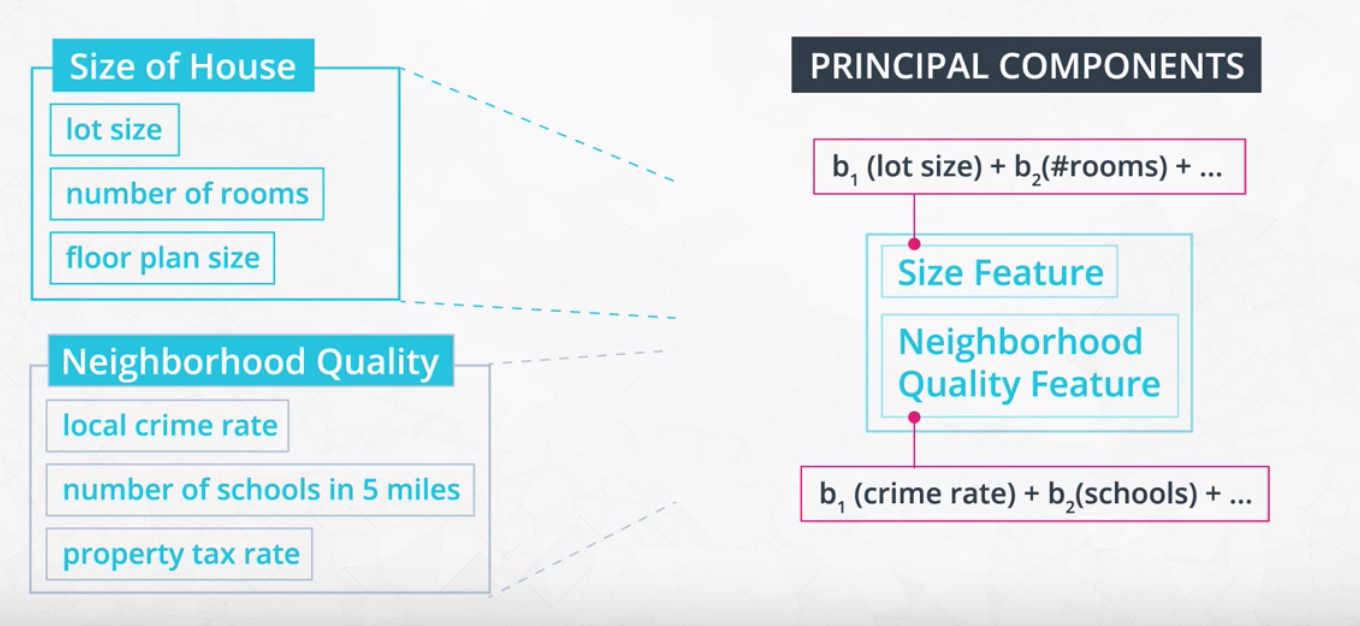
# Dimensionality Introduction

PCA are linear combination of the original features in a dataset. PCA is a latent feature

properties of PCA:

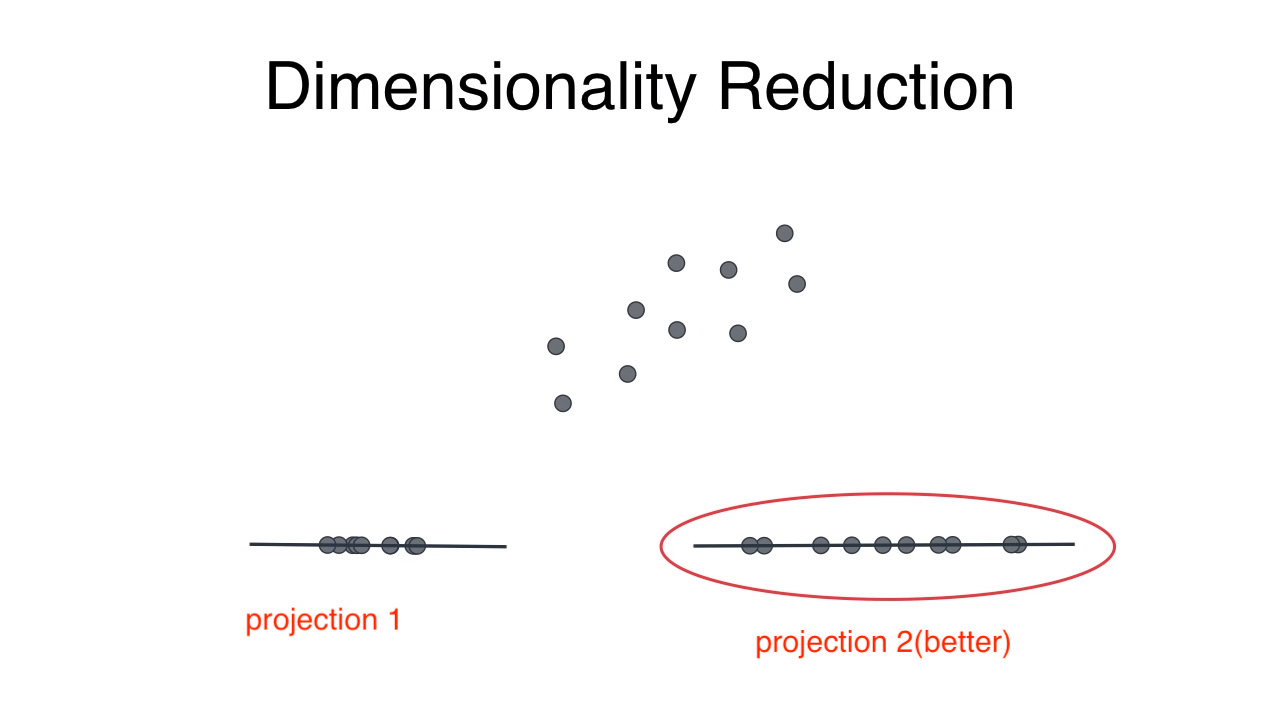
  • each component captures the largest amount of variance left in the data 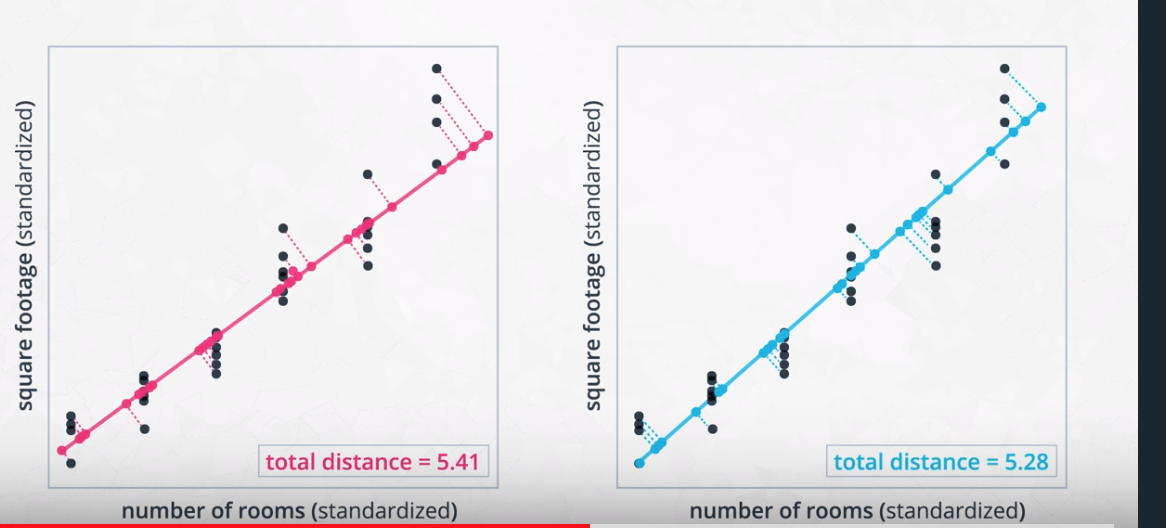So, PCA will choose the image in the right
  • components are othoganl to each other

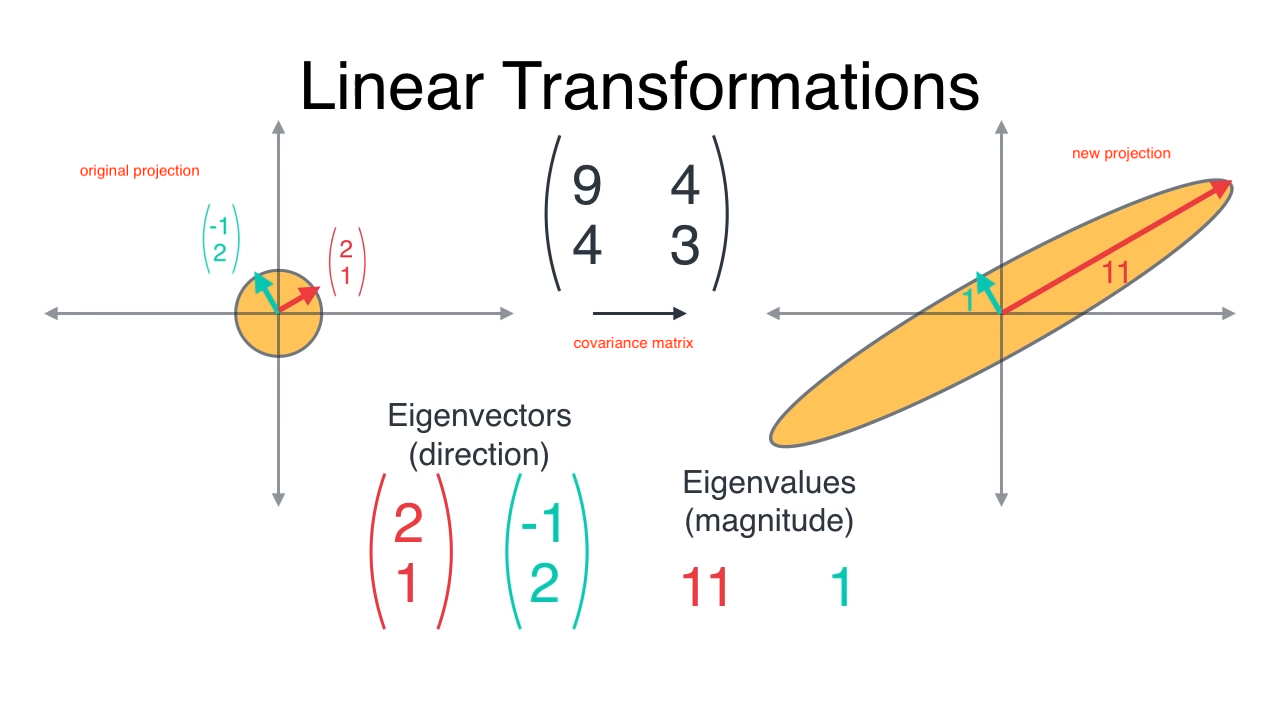
An eigenvalue is the same as the amount of variability captured by a principal component, and an eigenvector is the principal component itself.

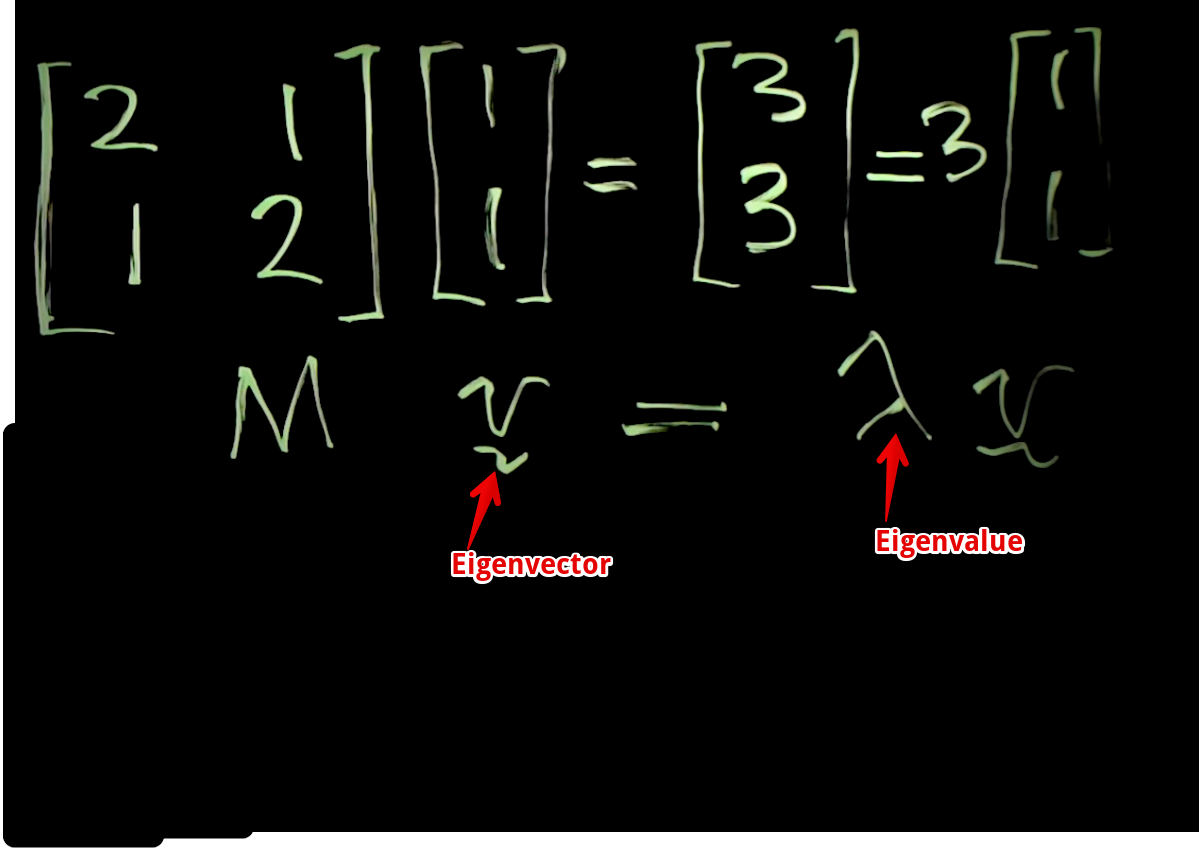
# Scikit-learn

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)

#instantiate
clf = RandomForestClassifier(n_estimators=100, max_depth=None)

#fit
clf.fit(X_train, y_train)

#predict
y_preds = clf.predict(X_test)



X = StandardScaler().fit_transform(data)
pca = PCA(n_components)
X_pca = pca.fit_transform(X)

pcs.explained_variance_ratio_
#Percentage of variance explained by each of the selected components.

# Visual

Converting 2D to 1D Here we find the best line

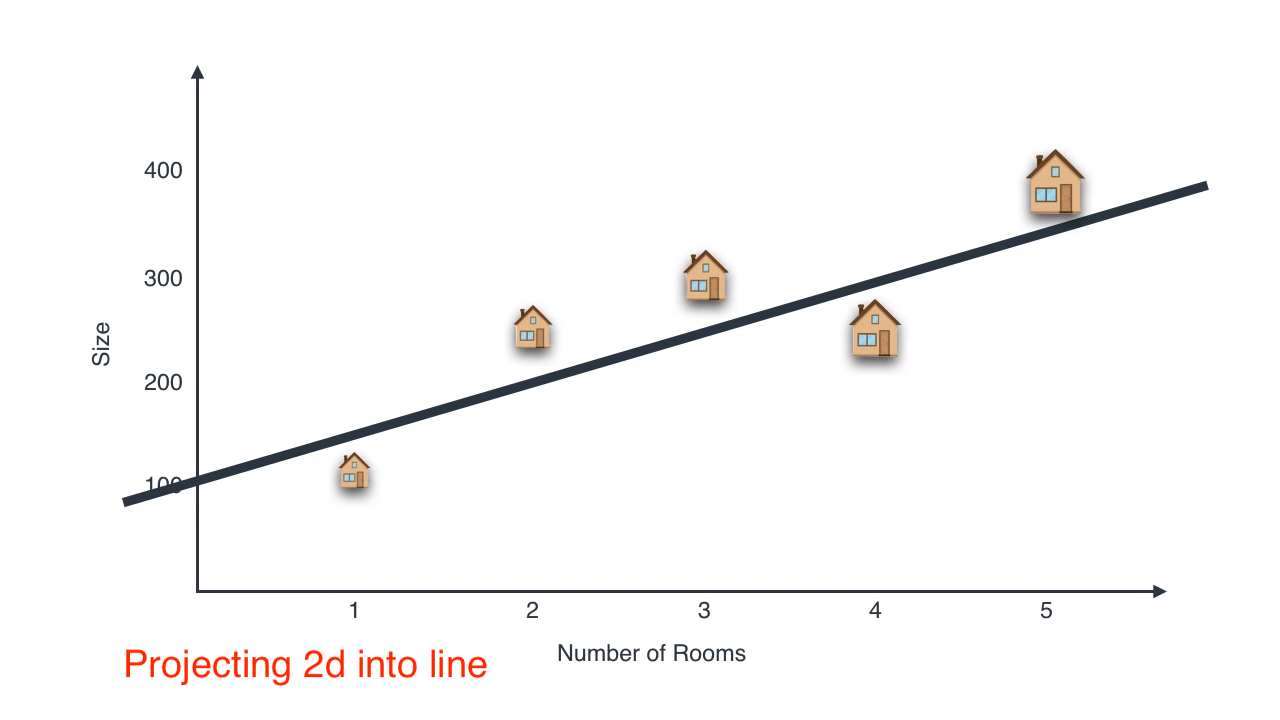
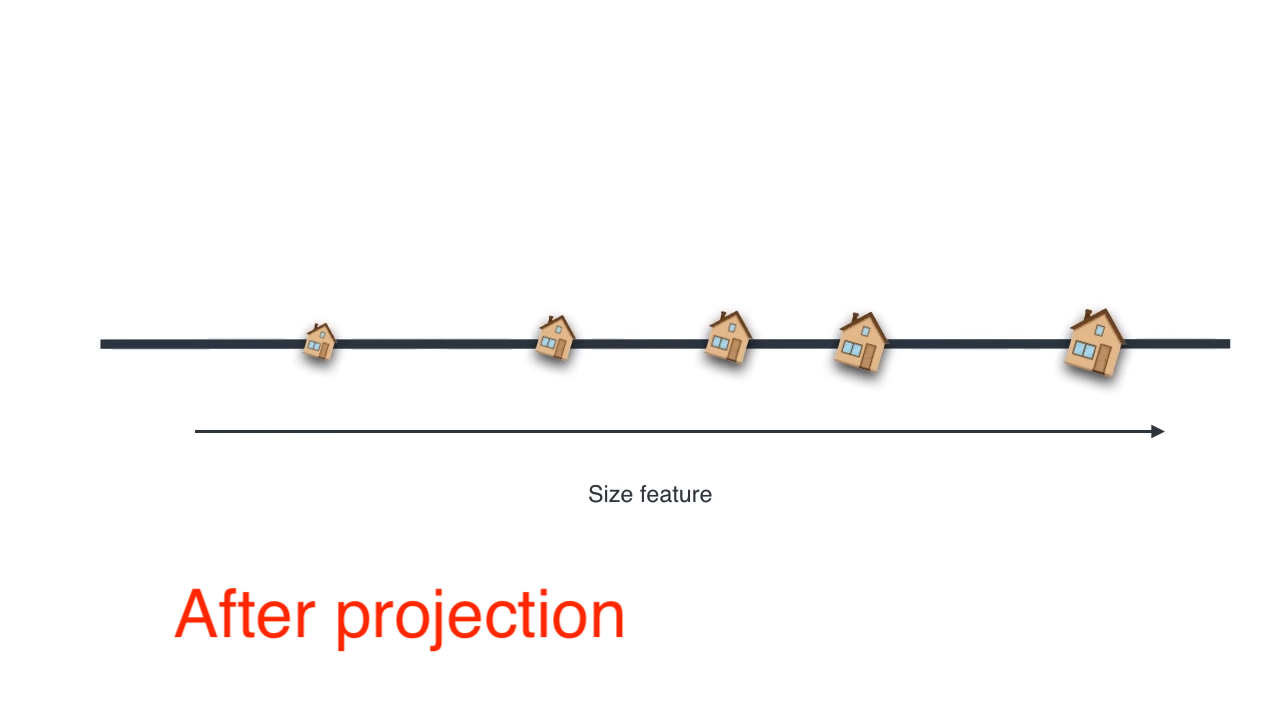
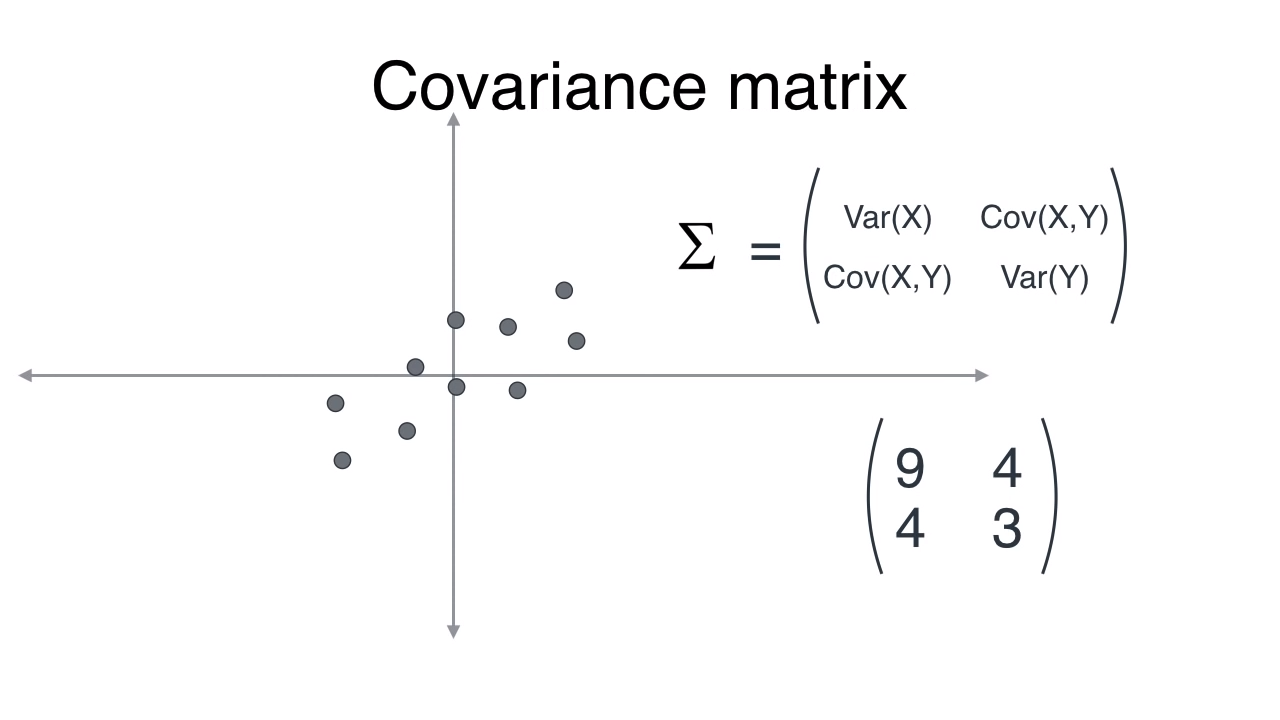
Linear Transformations

PCA with eigen vectors and eigen values

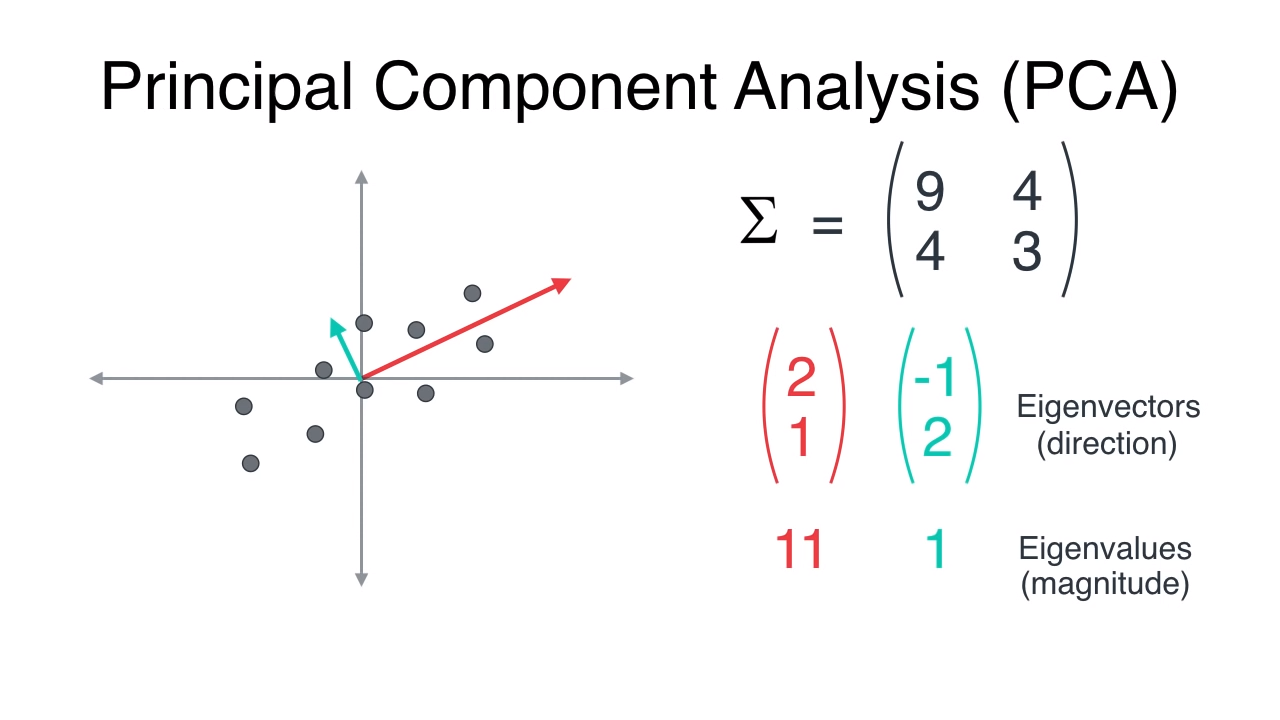
PCA Final visualization: 5D is projected to 2D

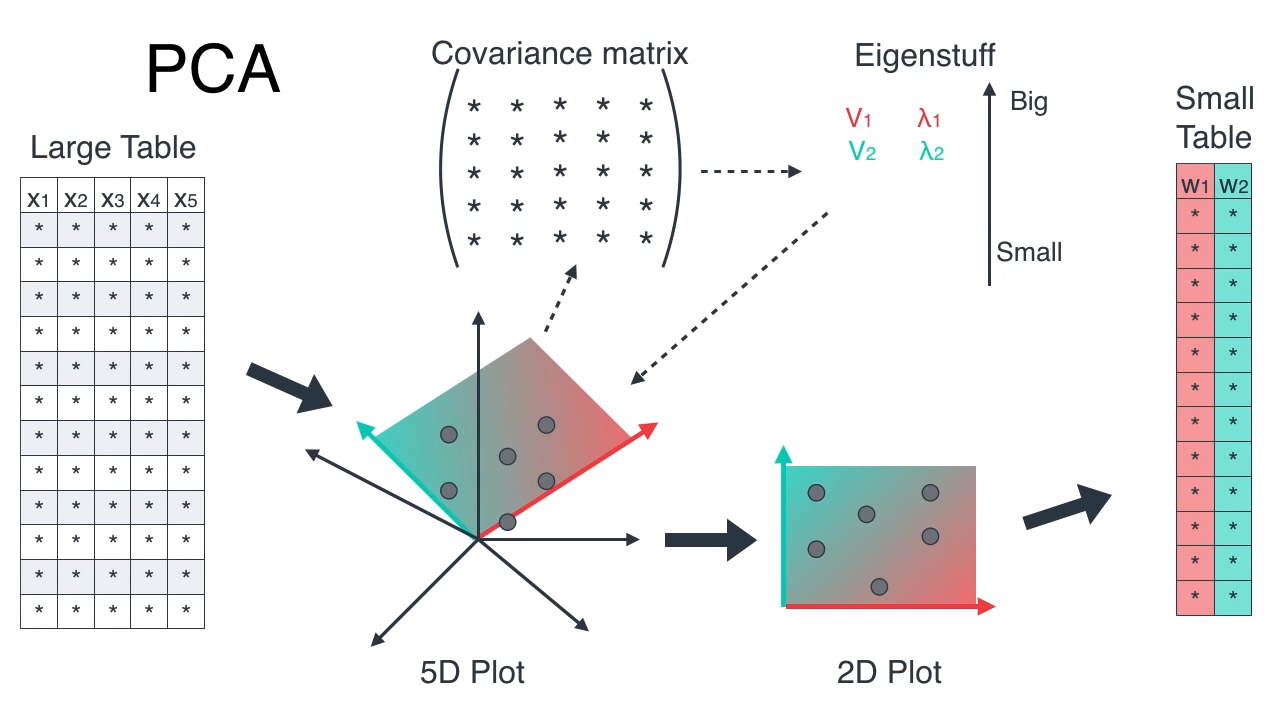
Other Notes:

  • PCA components tells us for each component, how much of the original feature is part of

Scree Plot tells how much variance is explained by each component.

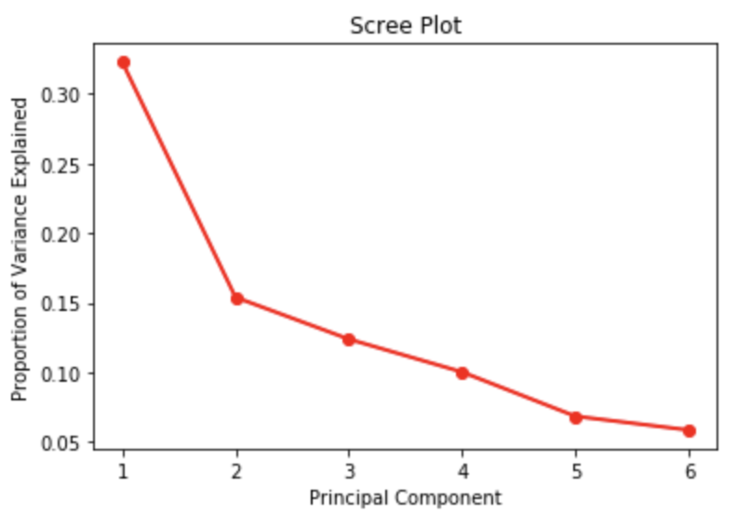
Ref:

  • https://www.youtube.com/watch?v=HH8pouRwphA
  • https://www.youtube.com/watch?v=PFDu9oVAE-g
  • https://sebastianraschka.com/Articles/2015_pca_in_3_steps.html
  • http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf
  • https://stats.stackexchange.com/questions/2691/making-sense-of-principal-component-analysis-eigenvectors-eigenvalues

← Singular Value Decomposition (SVD) →