My Notes

# Other Methods

Other clustering methods: Hierachial Clustering : Gives a visual indication of clusters relate to each other.

Density Based Clustering (like DBSCan)

  • robust against noise
  • doesn't need to specify number of K

# Hierachial Clustering

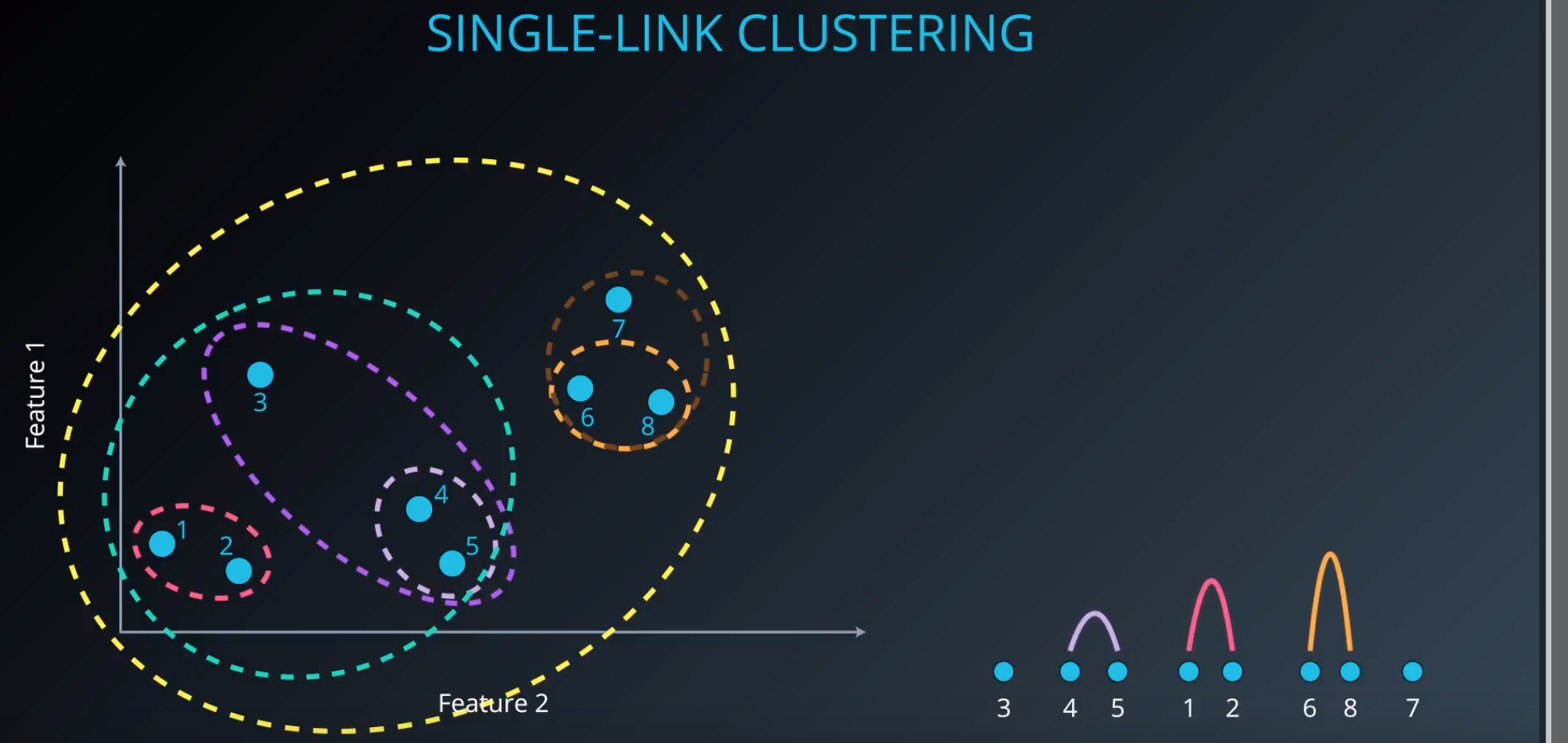
Algorithm

  1. Compute the distance between each and every point in the dataset (assumes every point is in it own cluster)
  2. Select the 2 closest point and group into a cluster
  3. Mark the result in a dendogram
  4. Repeat steps again until k is reached

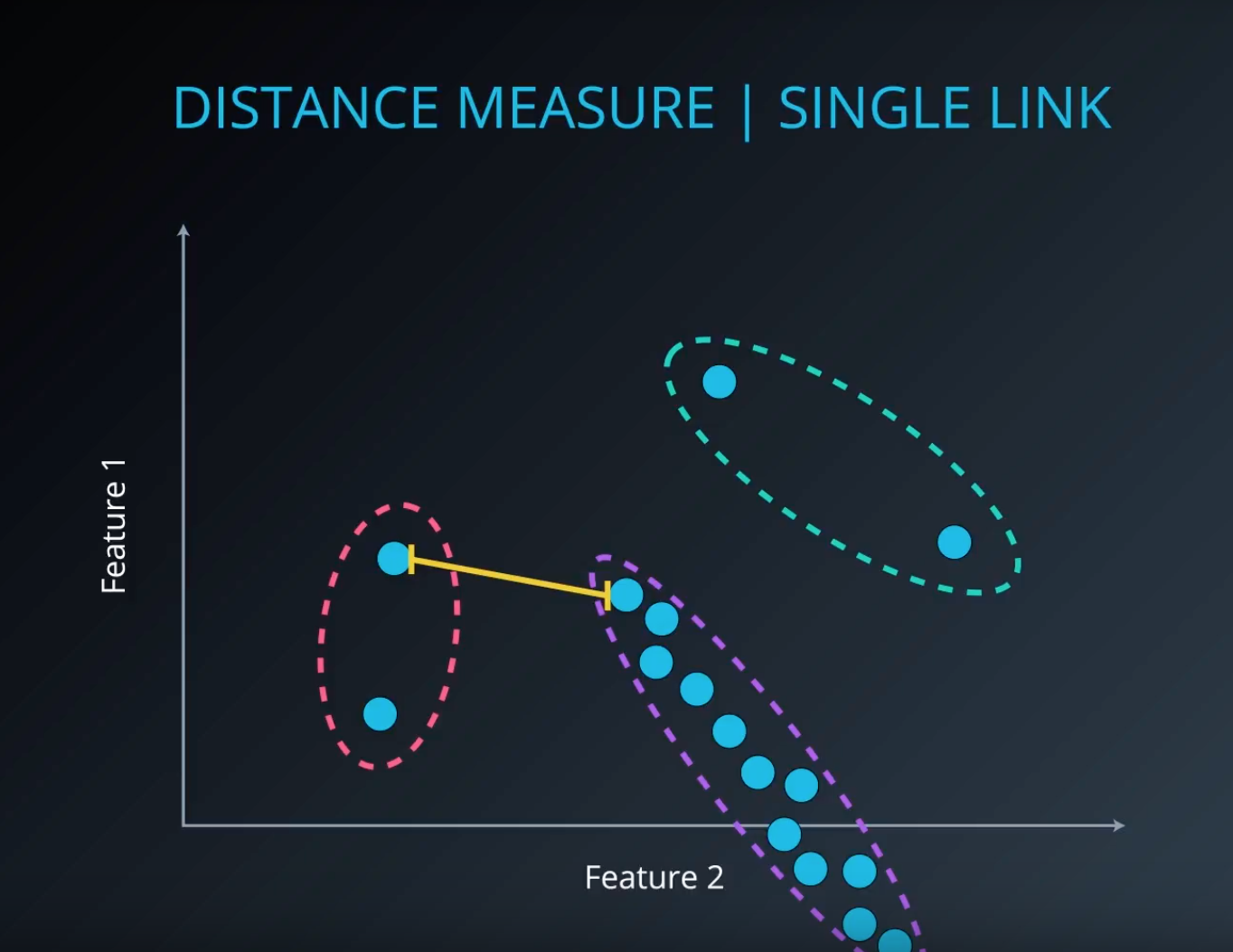
When comparing the distance between the point and the point from the cluster, we use the distance between the nearest point.

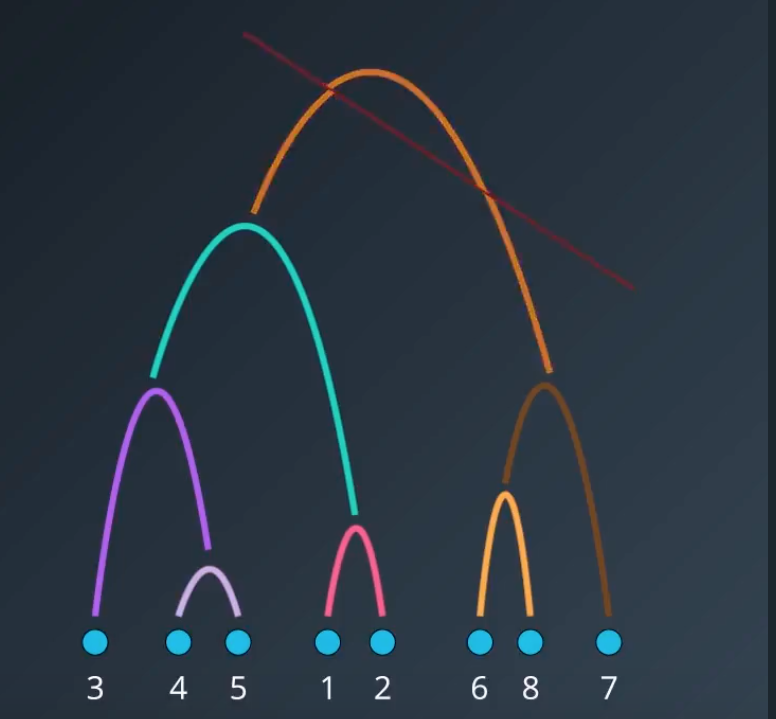
The end result of a Hierachial Clustering is a dendogram.

In order to have 2 clusters, then you would cut this tree.

Note: Hierachial Clustering methods differ in how they choose distance between clusters vs clusters.

Distance Metric:

One downside is that it creates elongated clusters.

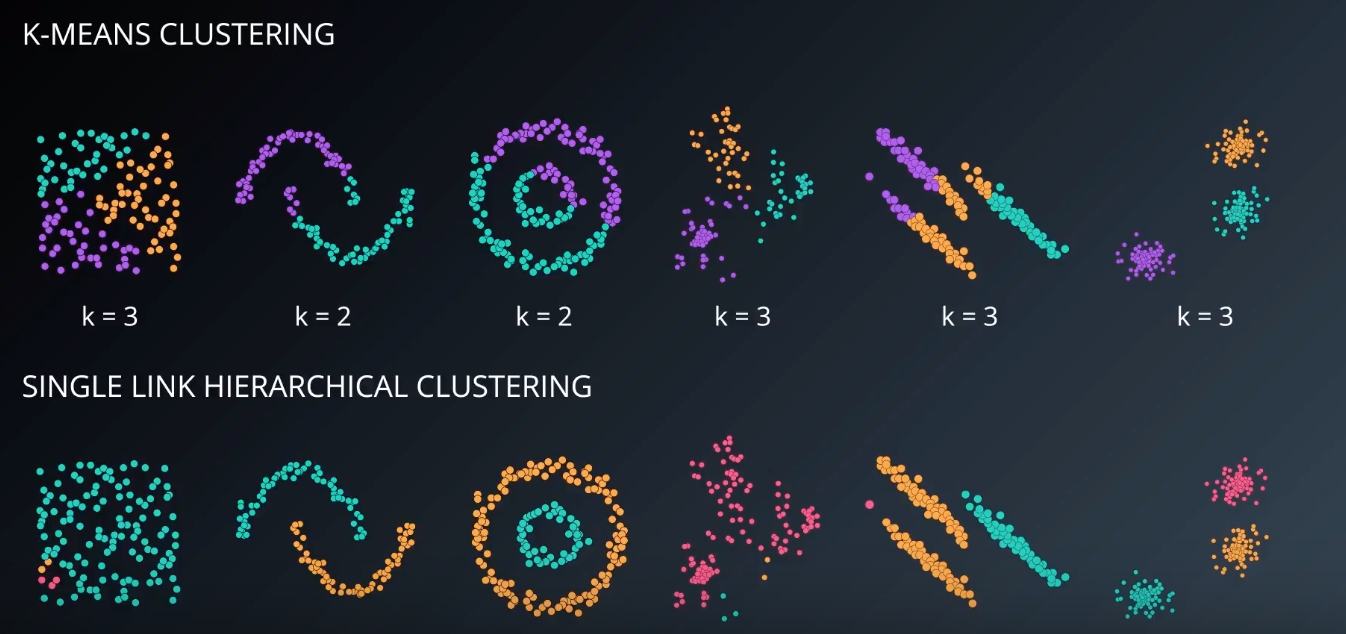For the first one, single link put it one big cluster For the fourth one also, it is one big cluster For the fifth one, it did a slighlty better job than k-means, but it did not come up with the 3 clusters.

One thing single link allows us to do is to gain additional insights from dendograms.

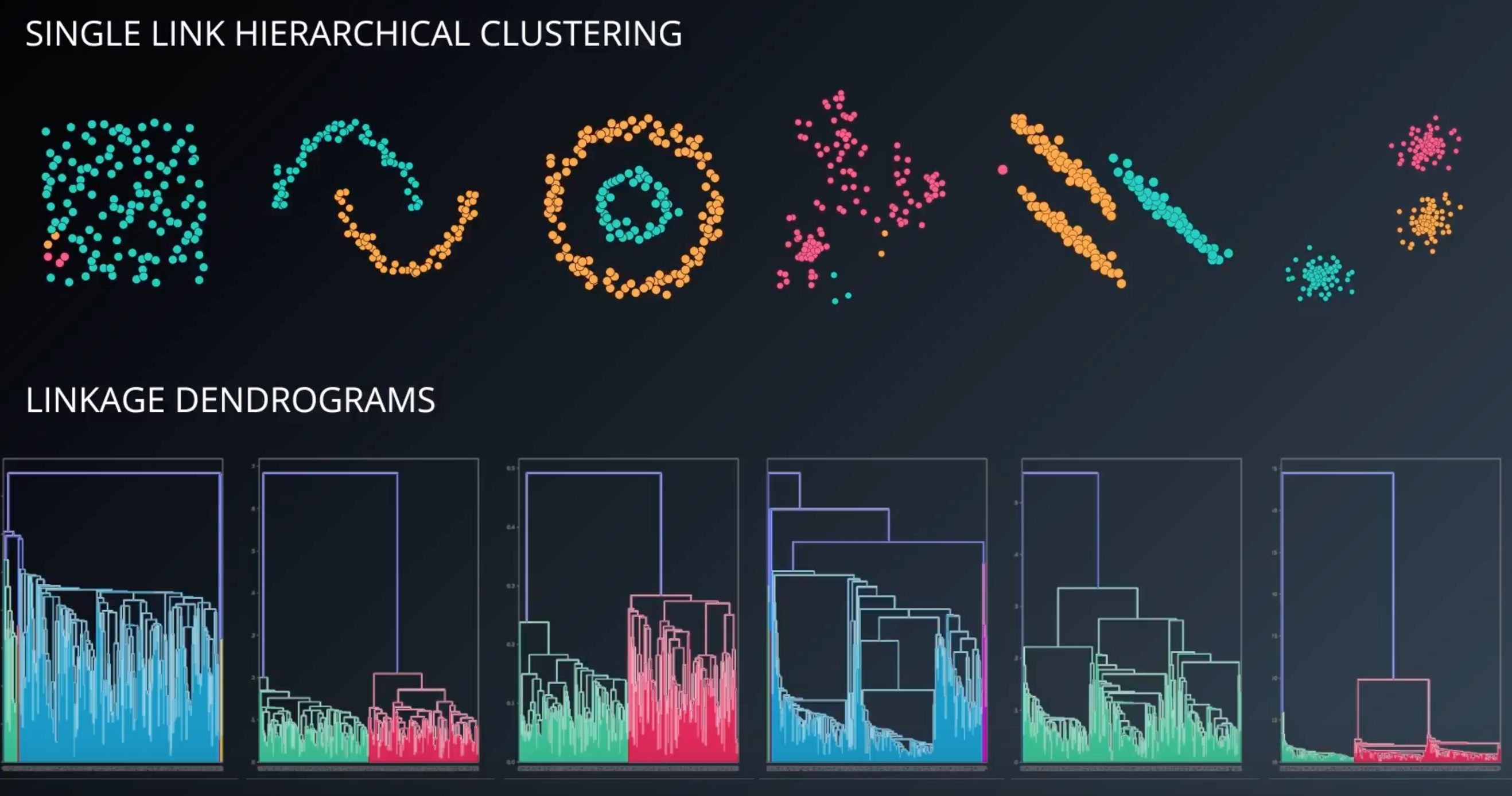
If you look at the fourth and fifth image, you can see that it can separate it into three clusters. So maybe a different run of the algorithm will come up with the optimal division.

# Alternatives to Single Link

Complete Link Similar to Single Link. Instead of using closest point, it uses the furthest point.

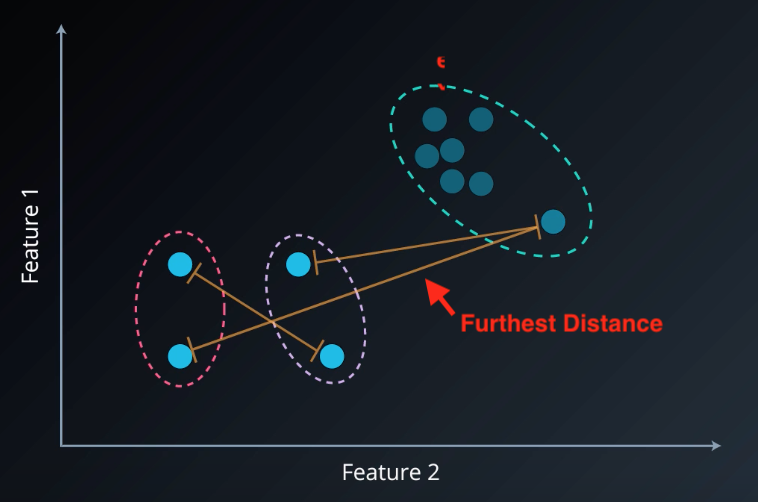
You can see that cluster 1 and cluster 3 distance is computed by its farthest point. However, in cluster 3 that point doesn't fully reflect the cluster.

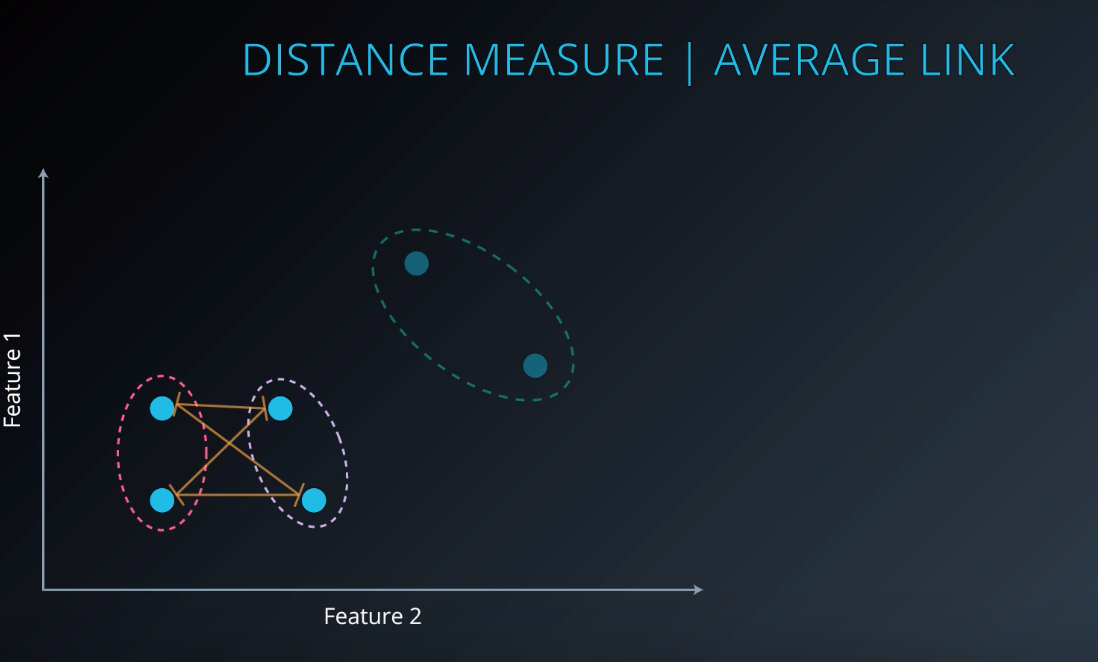
Average Link Clustering Take the average distance between all points of the cluster to all the other points of another cluster.

Wards Distance Default implementation in scikit learn

Find the center point (C_X) between cluster A and cluster B. Calculate the distance between all points of both clusters to C_X

Find the center point of Cluster A (C_A) and calculate all distance in Cluster A Find the center point of Cluster B (C_B) and calculate all distance in Cluster B

# Implementation

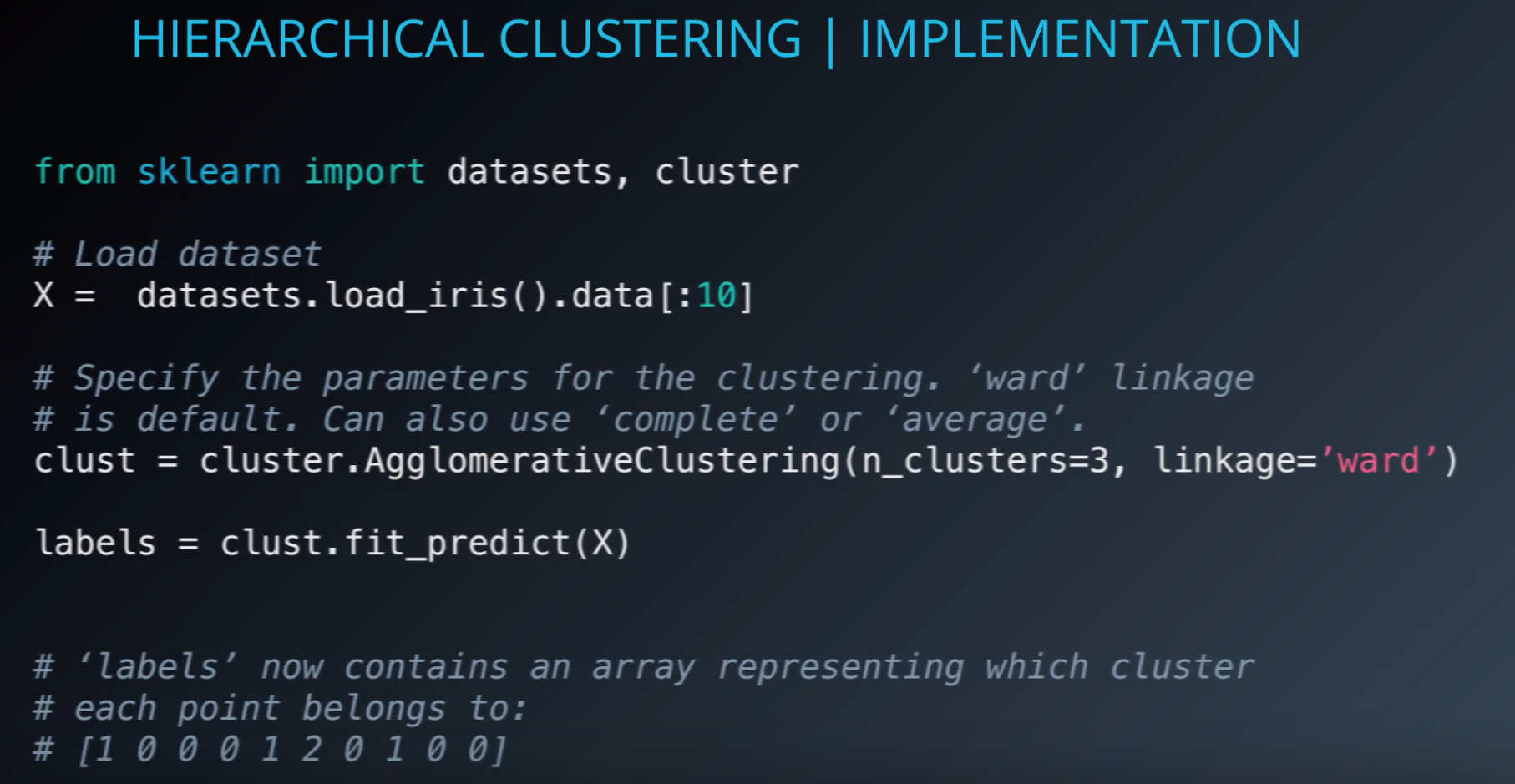
from sklearn import datasets
from sklearn.metrics import adjusted_rand_score
from sklearn import preprocessing


iris = datasets.load_iris()
# normalize by min
normalized_X = preprocessing.normalize(iris.data)

# default hierachial clustering
ward = AgglomerativeClustering(n_clusters=3, linkage='ward')
ward_pred = ward.fit_predict(normalized_X)

# external cluster validation index which results in a score between -1 and 1, where 1 means two clusterings are identical of how they grouped the samples in a dataset 

adjusted_rand_score(iris.target, ward_pred)

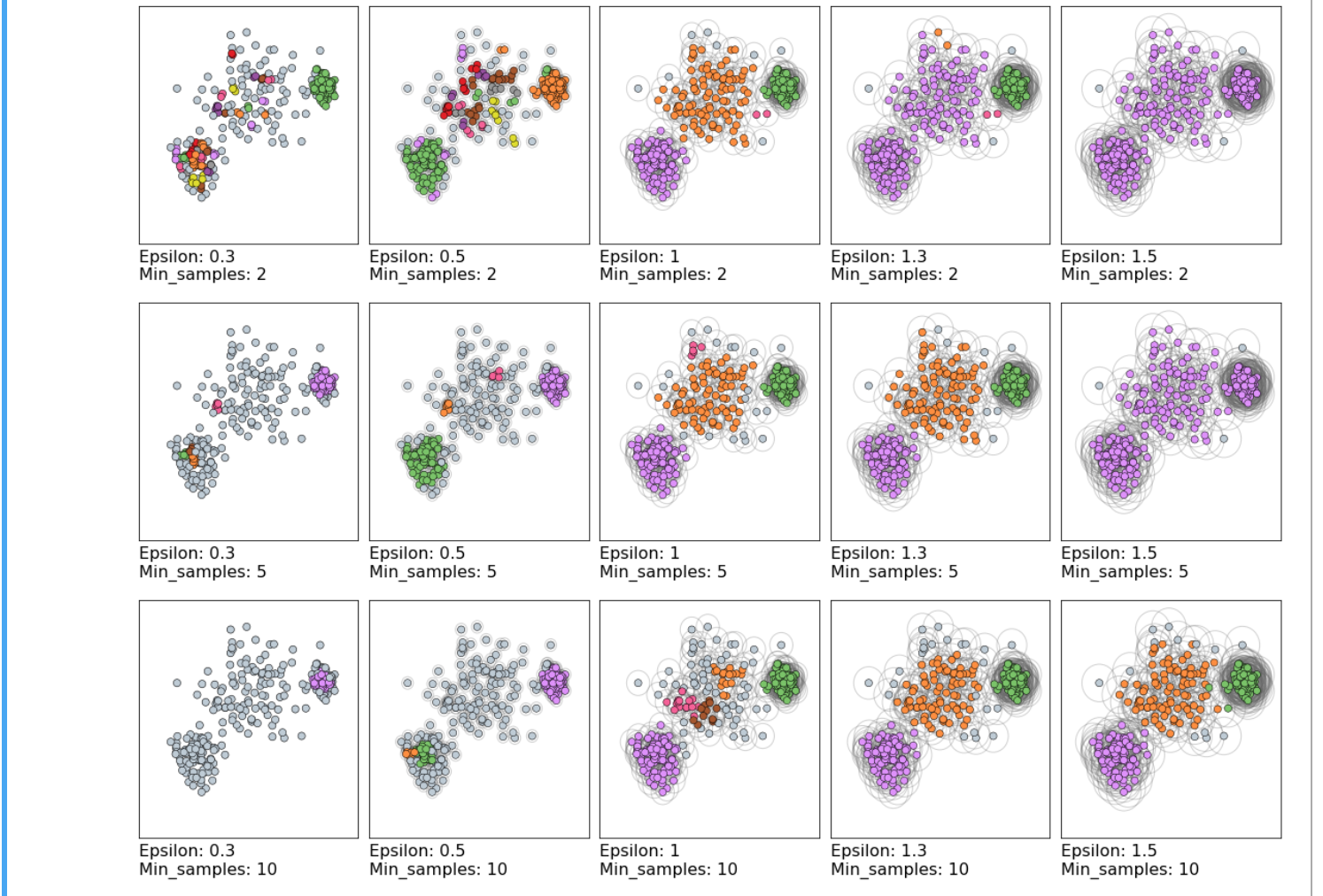
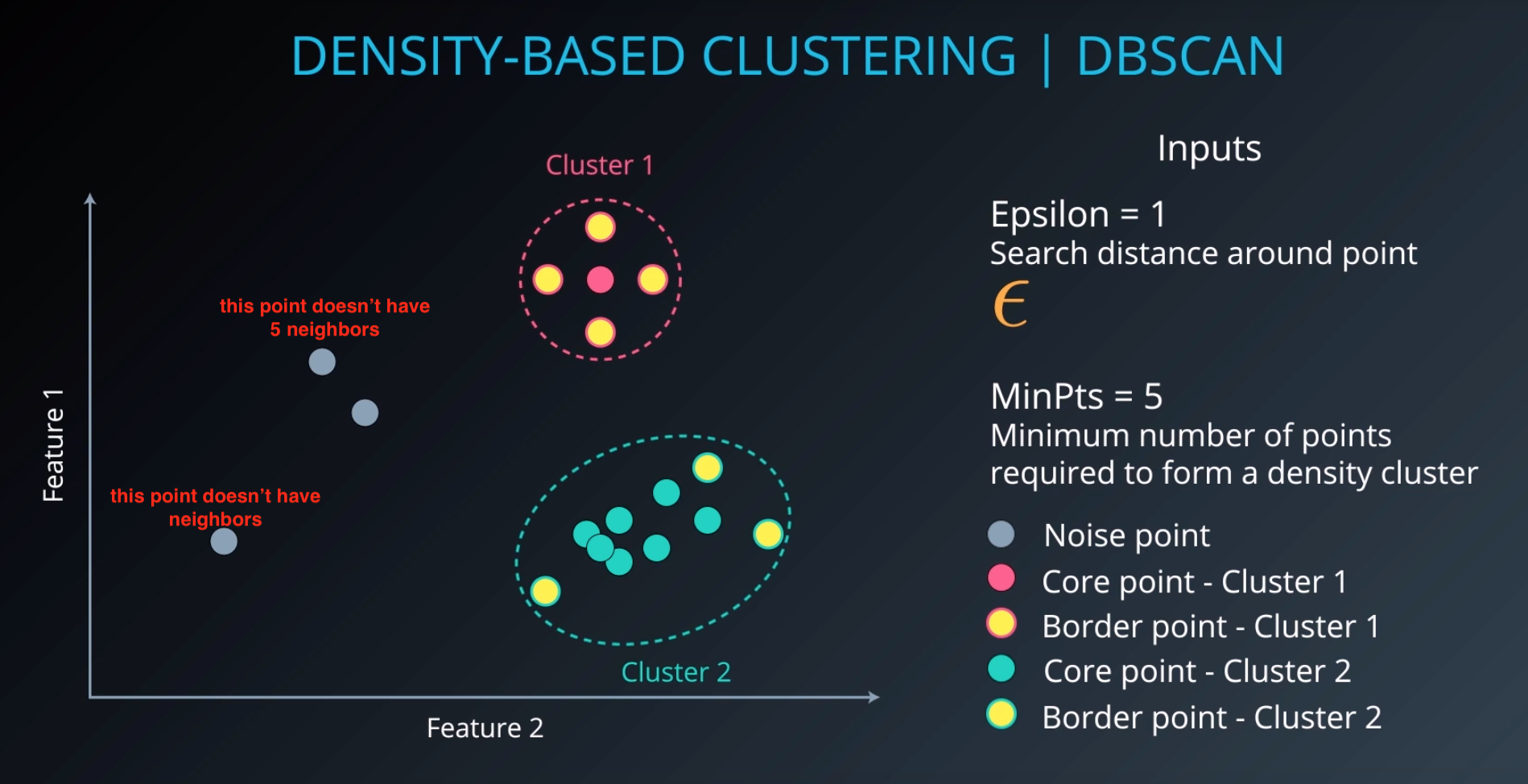
# DBScan

Density Based Spatial clustering of applications with noise.

Not every point will be part of a cluster

# Comparision with Kmeans

# Implementation

from sklearn import cluster
epsilon=2.2
dbscan = cluster.DBSCAN(eps=epsilon, min_samples=5)
clustering_labels_2 = dbscan.fit_predict(dataset_1)

Comparision How epsilon and min sample interact

← PCA →