Gaussian Mixture Models

"Soft" Clustering Algorithm

Every point is part of every cluster with a percent

Gaussian Distribution

One Dimension

μ ± 1σ = 68% data μ ± 2σ = 95% data μ ± 3σ = 99% data

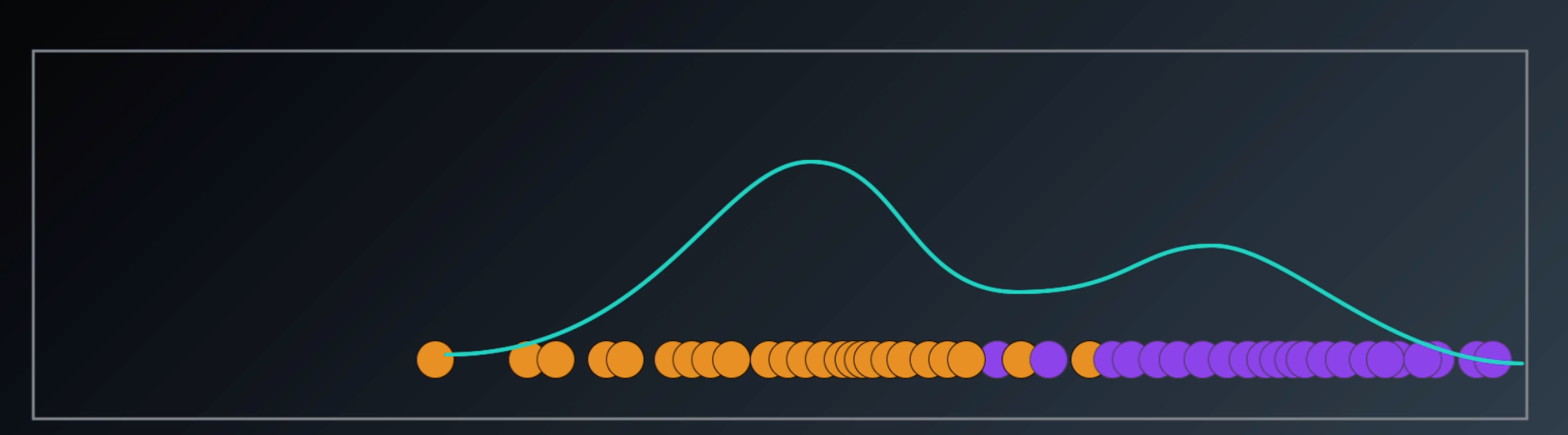
Can be a combination of multiple gaussian distribution

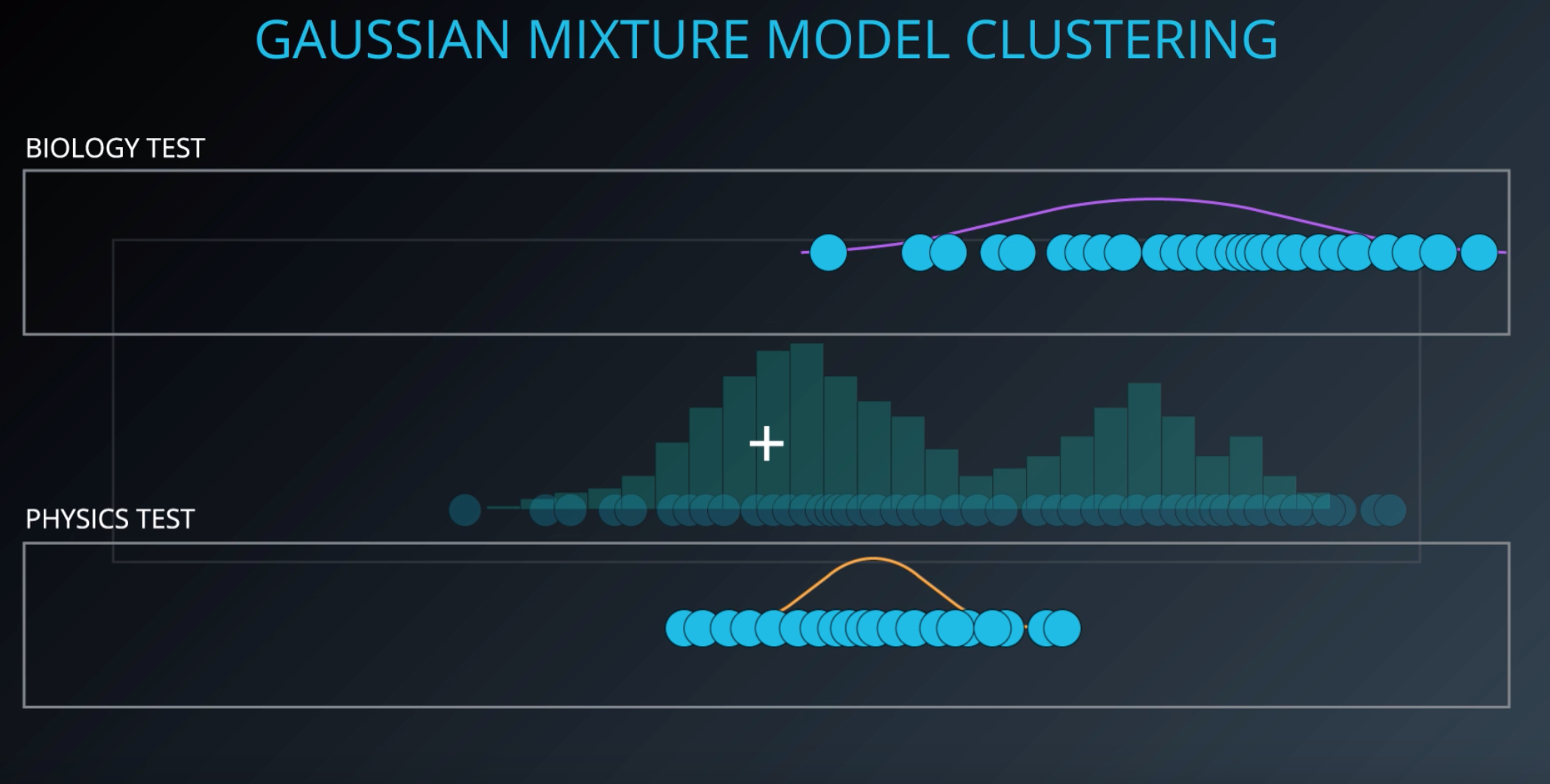
Scikit Learn will find that there is two gaussian

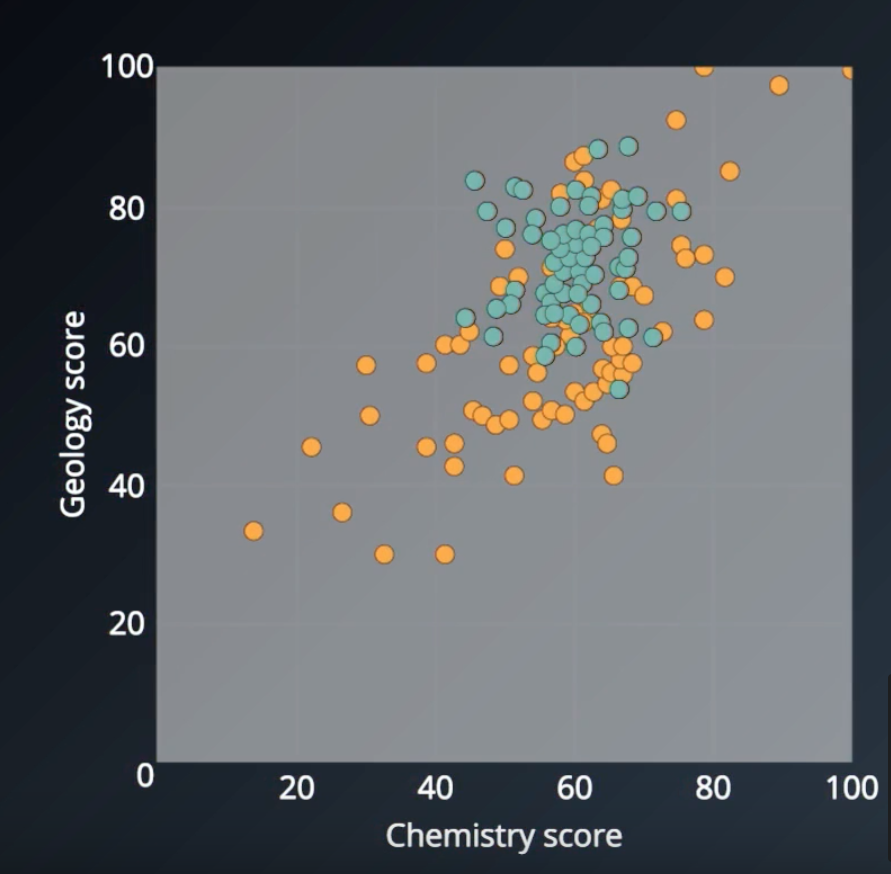
Two Dimension In the below image, each subject is its own gaussian

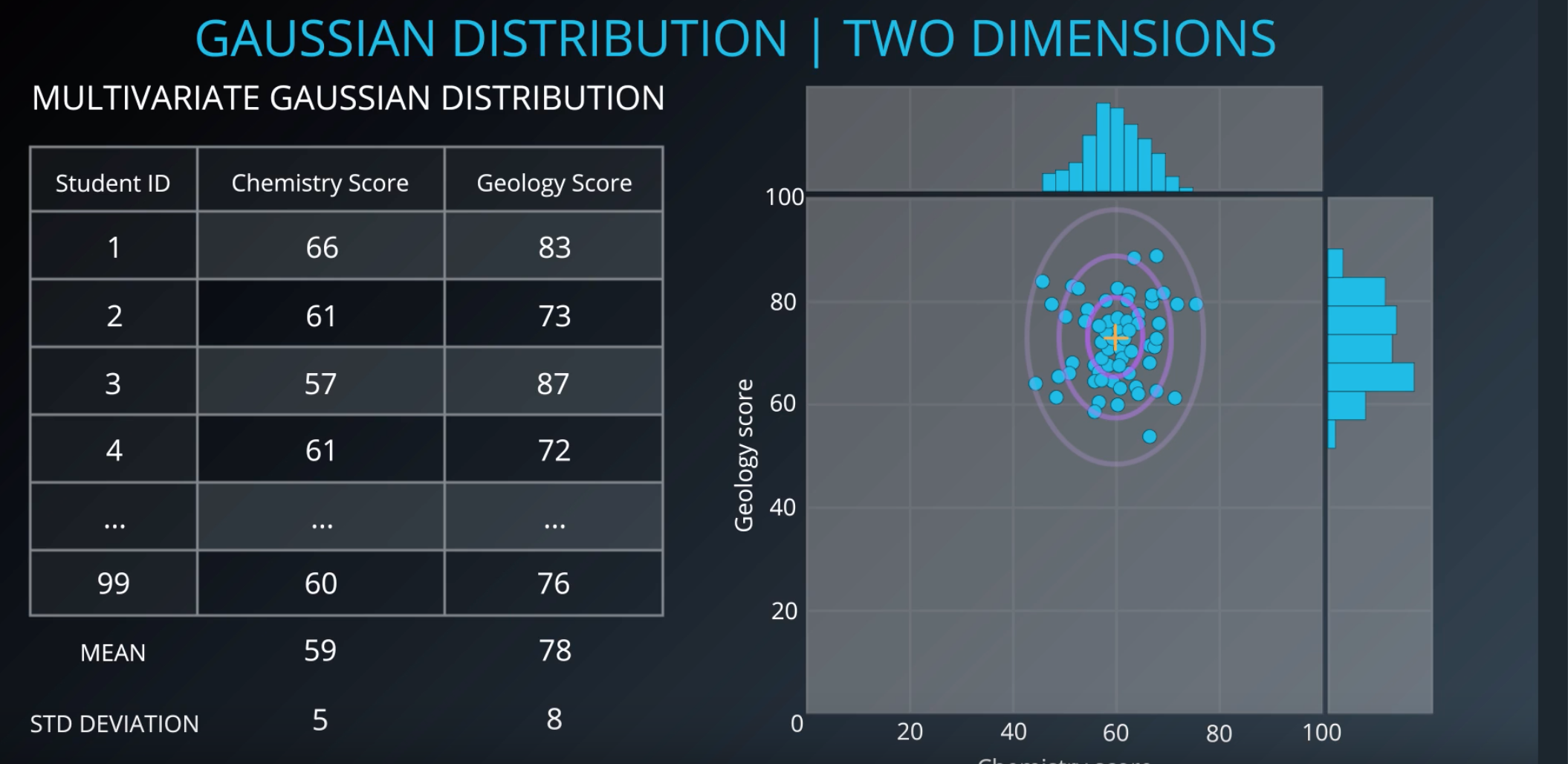
Multiple 2D Gaussian Scores for chemistry/geology for class of 2016 and 2017

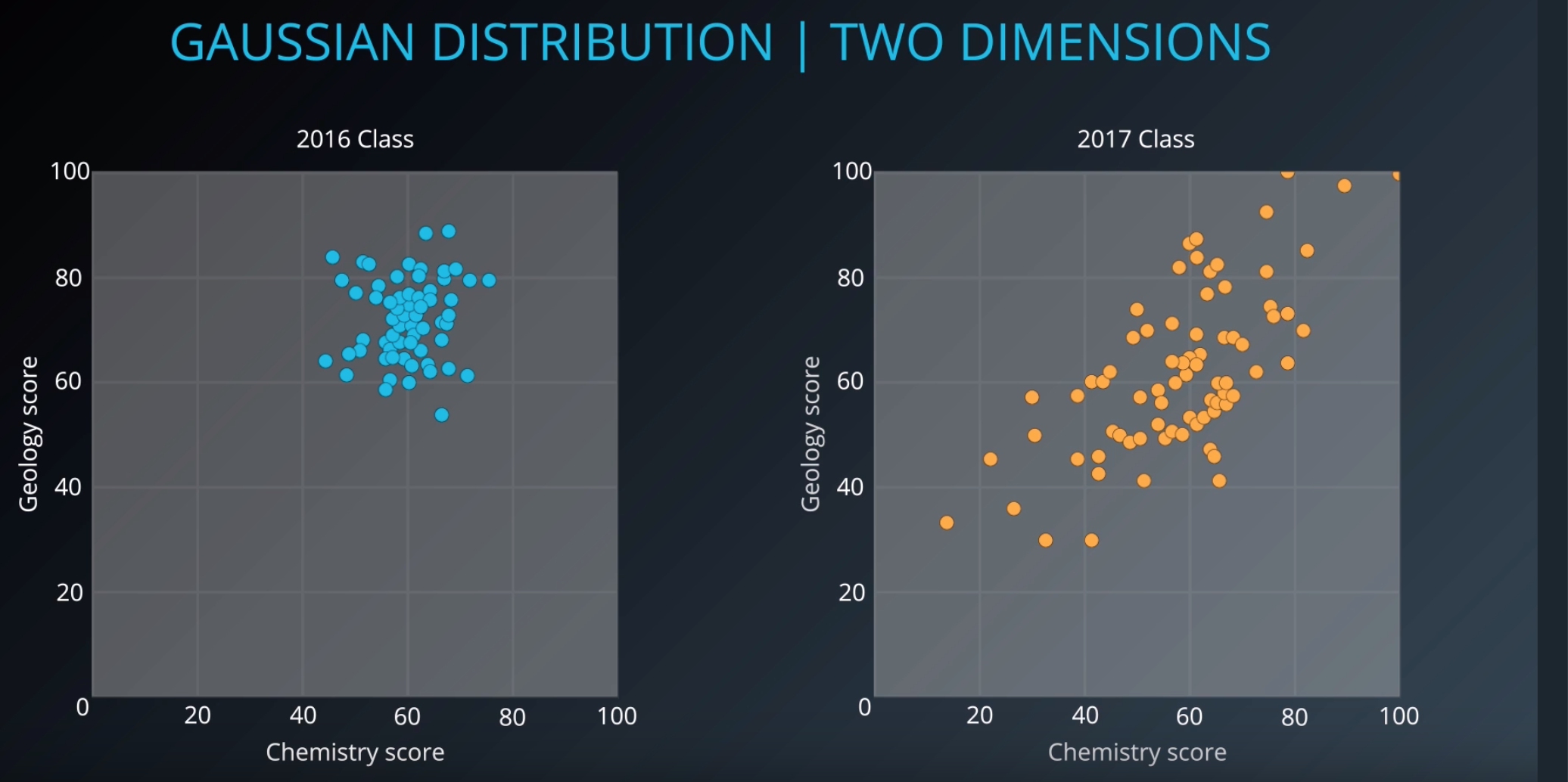
Even if we combine both gaussian mixtures, gmm can separate them

Expectation Maximization

Steps:

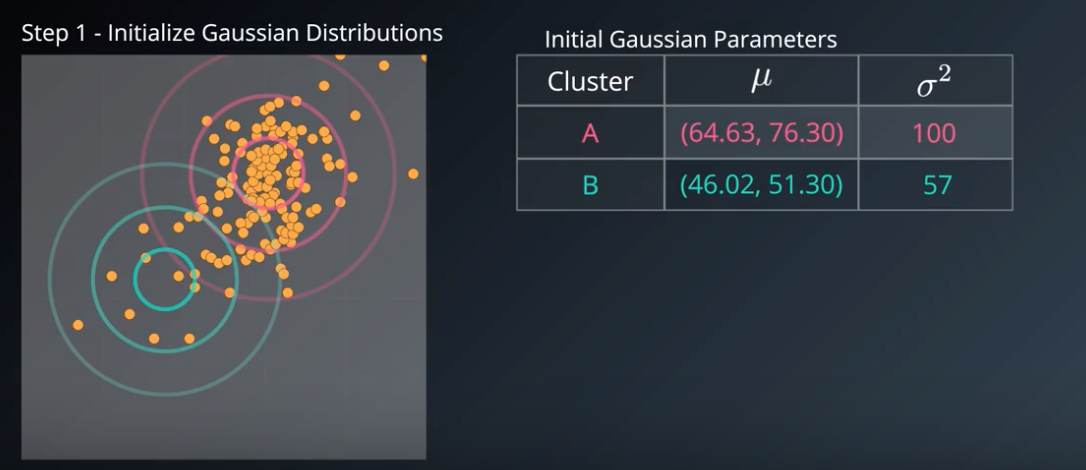
1. initialize K Gaussian Distributions
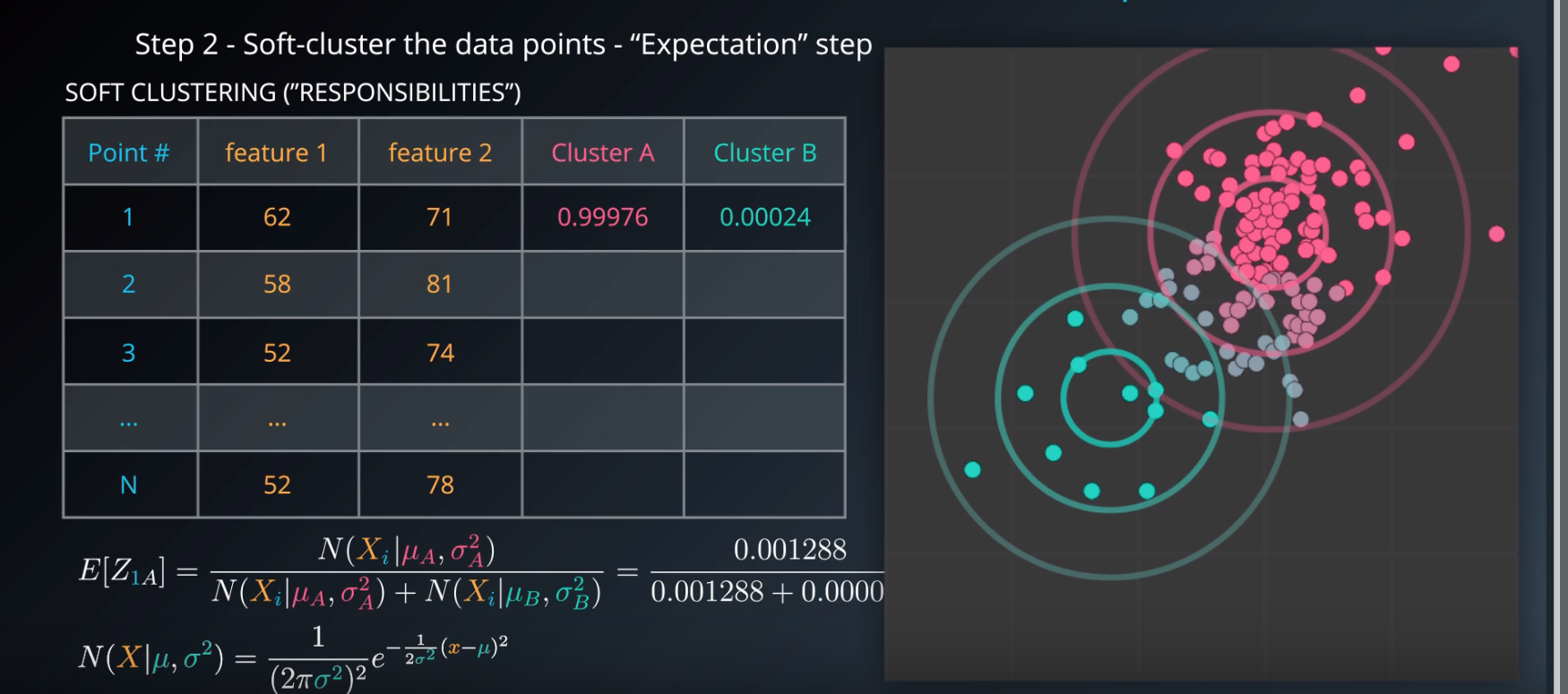
2. soft-cluster data "expectation"
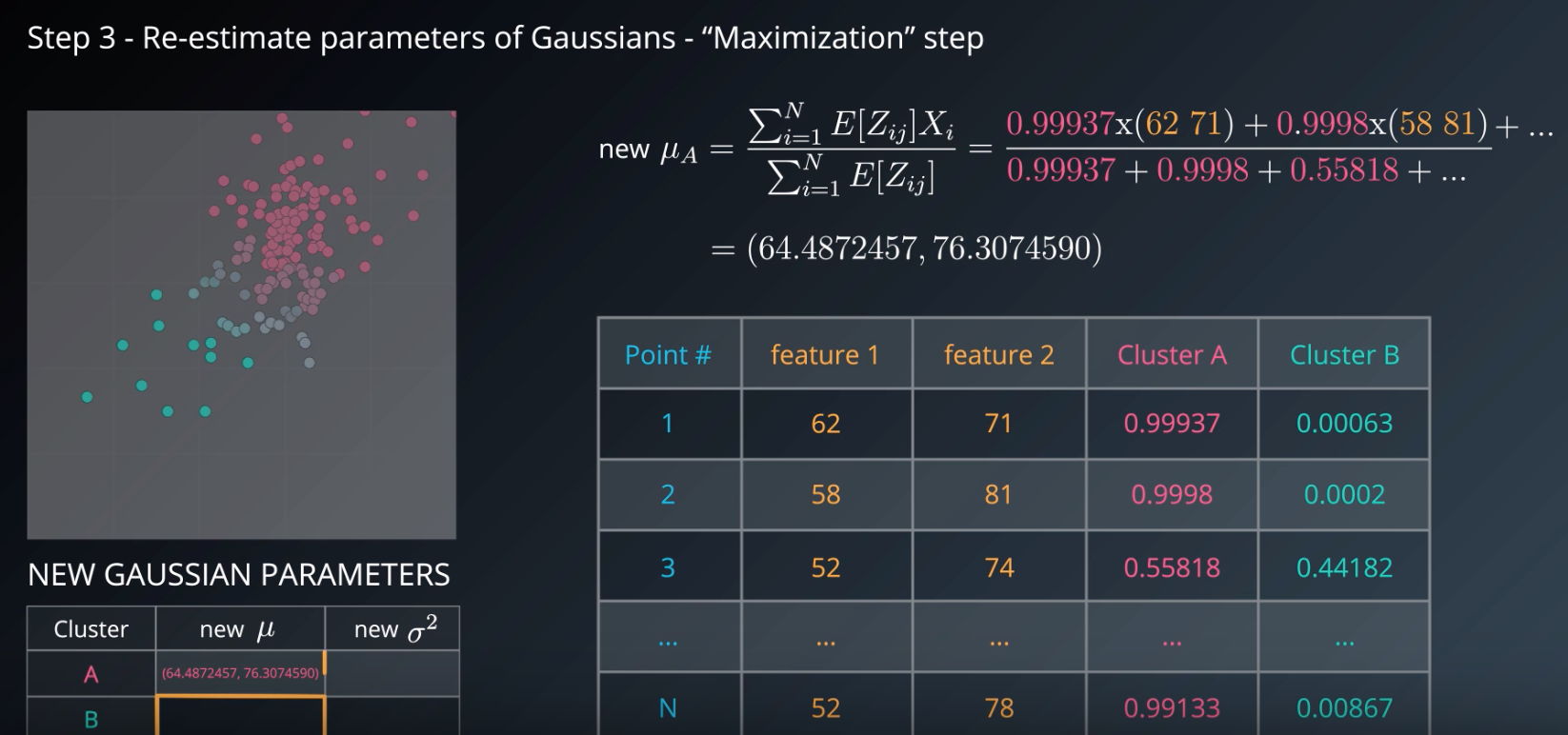
3. re-estimate the parameters of the guassians "maximizaion"
4. evaluate log likelihood to check for convergence
5. Repeat from setp 2 until converrged

Step 1

Step 2

Step 3

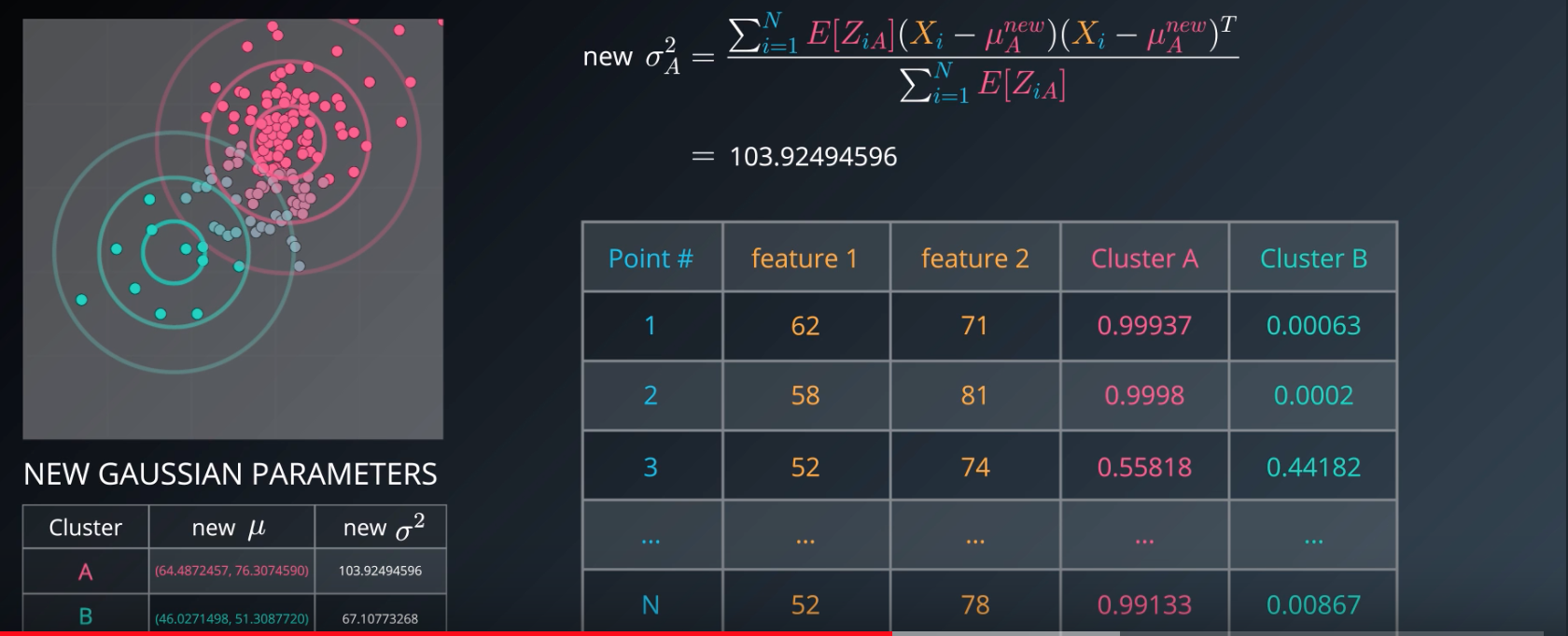
Step 4 higher the number, more sure the mixture model fits the data

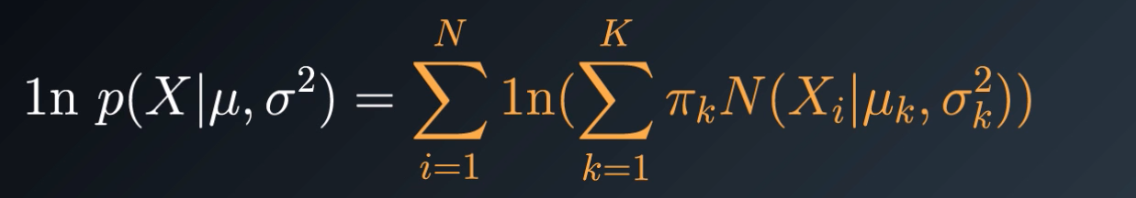
Iterative Steps

step 0: start with random gaussians

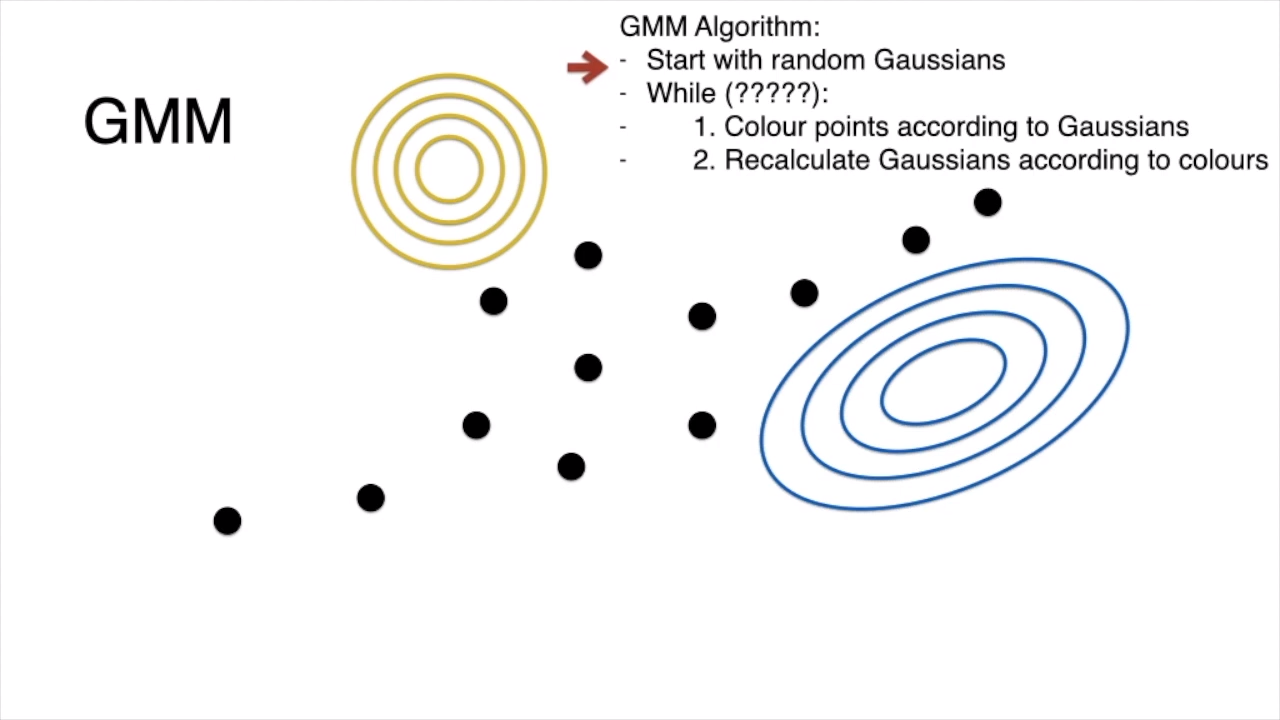
step 1: assign points according to gaussian

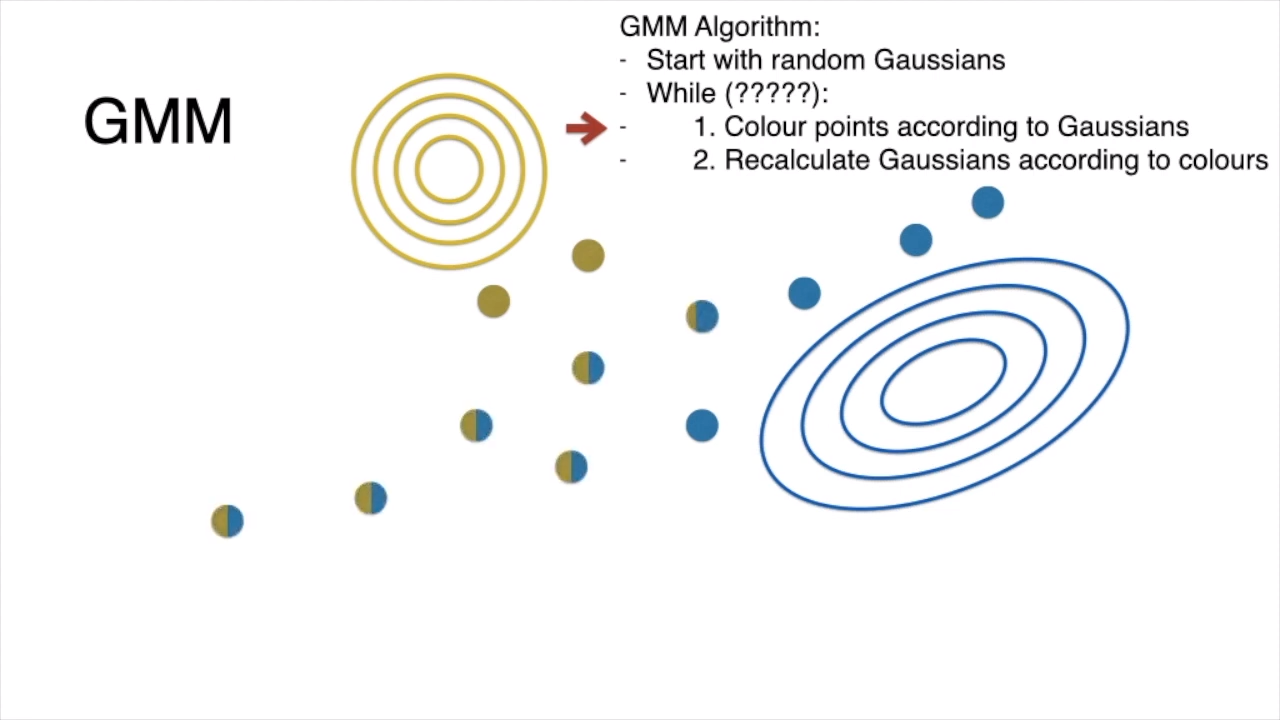
step 2: recalculate gaussian

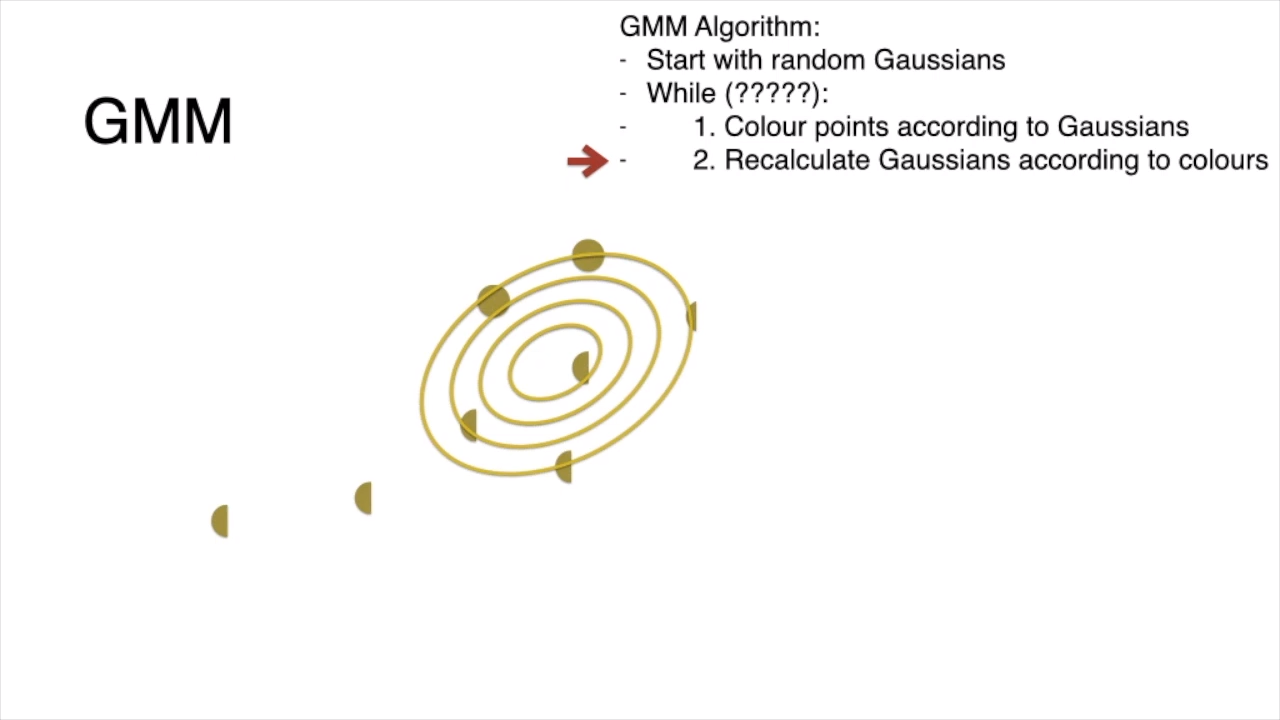
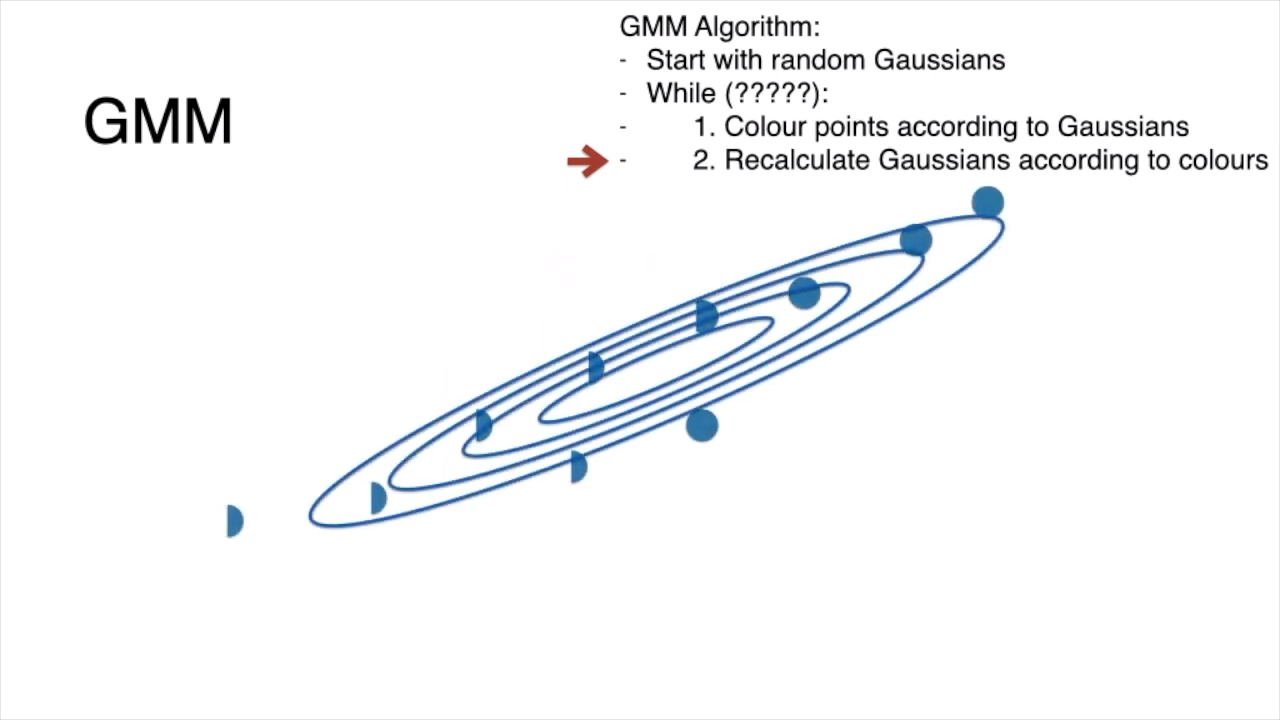
anf then repeat steps 1 and 2 again

All steps visually shown

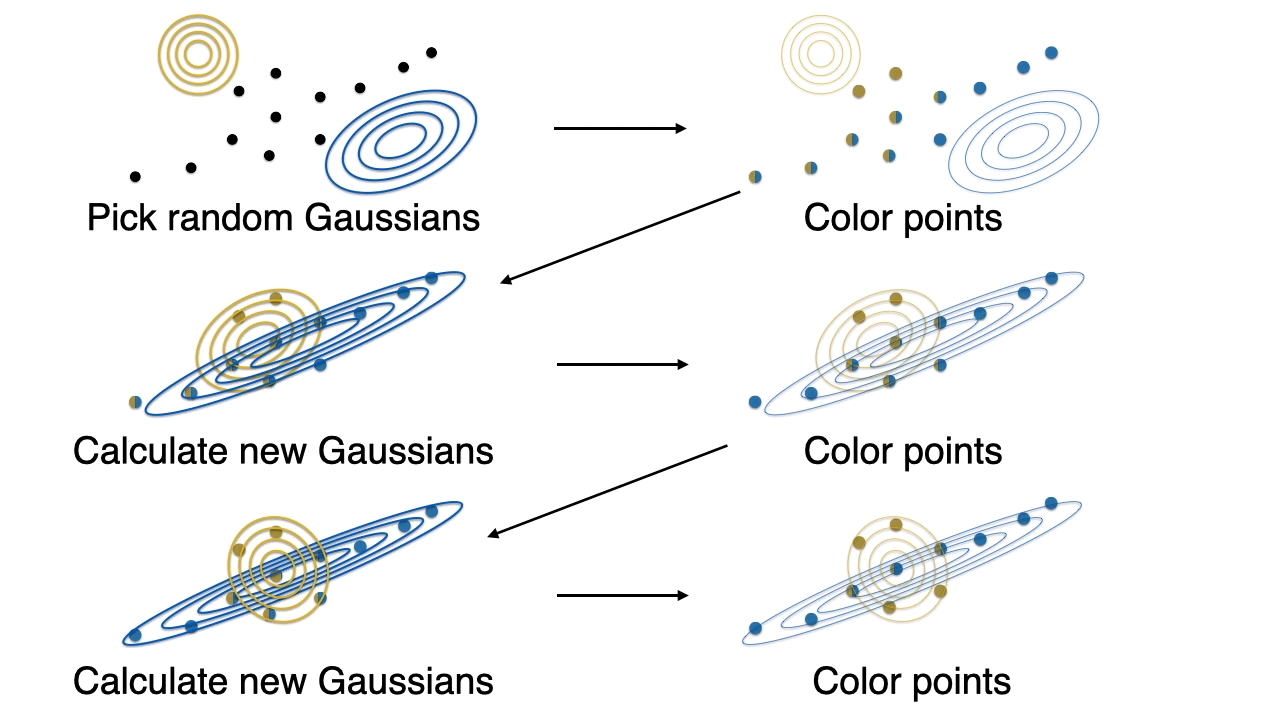
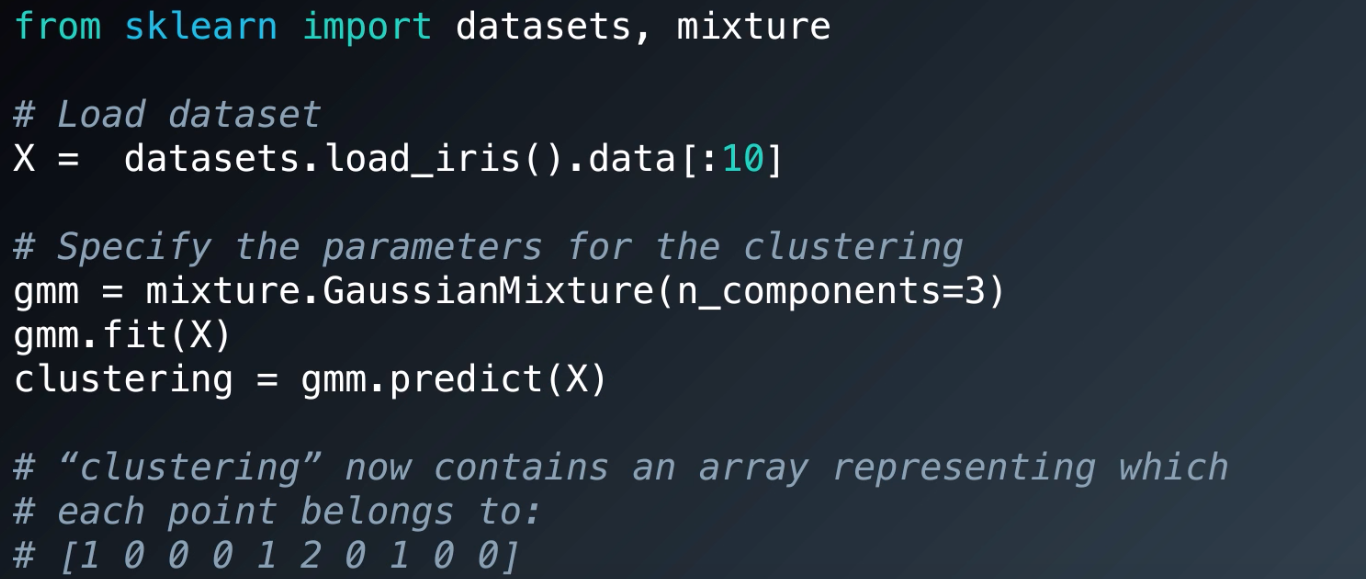
Implementation

Pros and Cons

Advantages:

• soft clustering (sample membership of multiple clusters)
• cluster shape flexibility

Disadvantages:

• sensitive to initialization values
• possible to converge to local optimum
• slow convergence rate

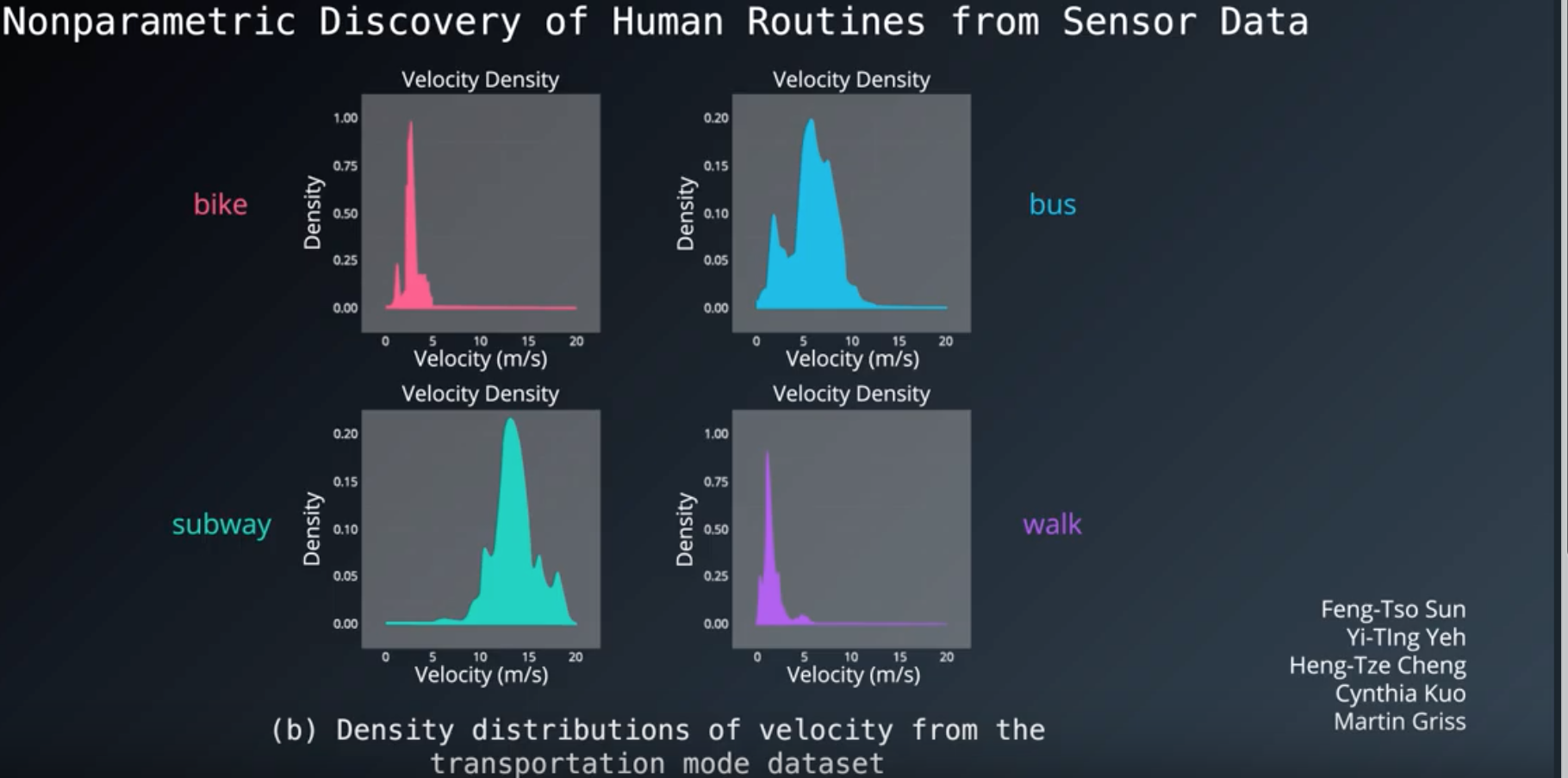
Applications

activity recognition from sensor data

background image subtraction feed streaming video to learn what is background Demo (opens new window)