Metrics

Root Mean Squared Error (RMSE)

Common perfomance measure metric for regression tasks.

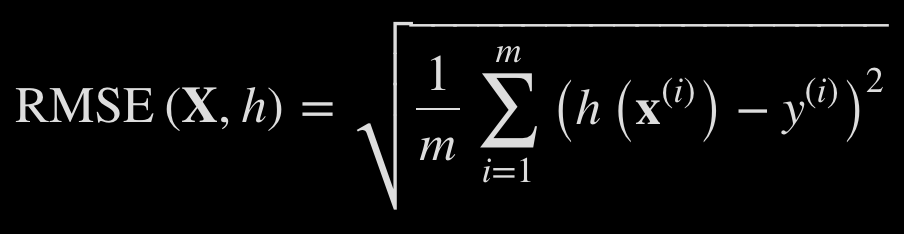
m = number of samples
x^i = vector of all feature values
h = prediction functions

Because we are squaring differences, RMSE is sensitvie to outliers.

Mean Absolute Error (MAE)

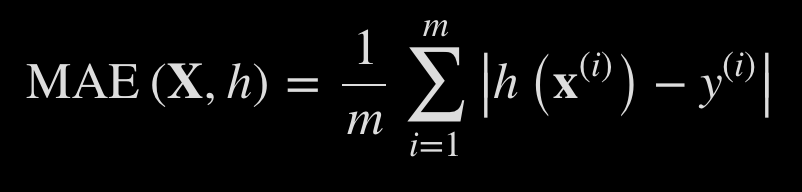
Similar to RMSE, but not squared. Less sensitive to outliers.

Confusion Matrix

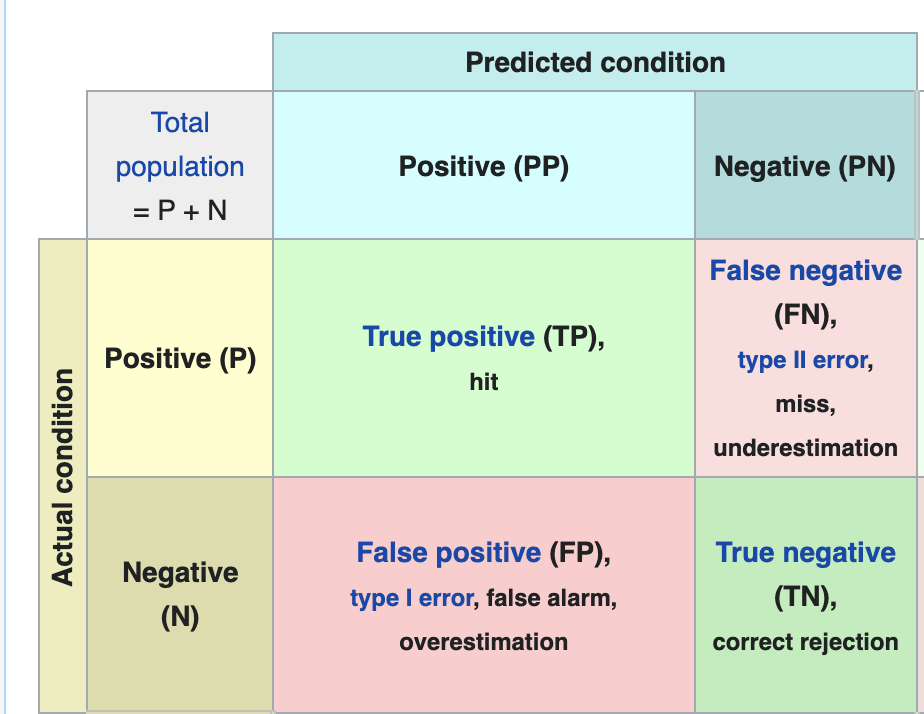
rows are actual classes, columns are predicted classes.

Image Reference: Wikipedia (opens new window)

>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)

Precision / Recall

precision

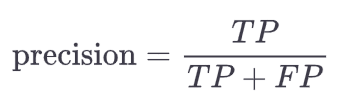
You can get perfect precision, by only making one single positive prediction and ensure it is correct.

so TP=1/1 and FP will be 0

recall

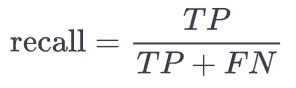
>>> from sklearn.metrics import precision_score, recall_score
>>> precision_score(y_train, y_train_pred) 
0.7290850836596654
>>> recall_score(y_train, y_train_pred) 
0.7555801512636044

You can plot precision and recall to decide what threshold to use.

F1 score

Single metric that combines precision and recall.

>>> from sklearn.metrics import f1_score
>>> f1_score(y_train, y_train_pred)

ROC Curve

Correlation

Standard Coorleation also calleds Pearson's r.

Range from -1 to 1. A correlation of 0 , just means that there is no linear correlation.

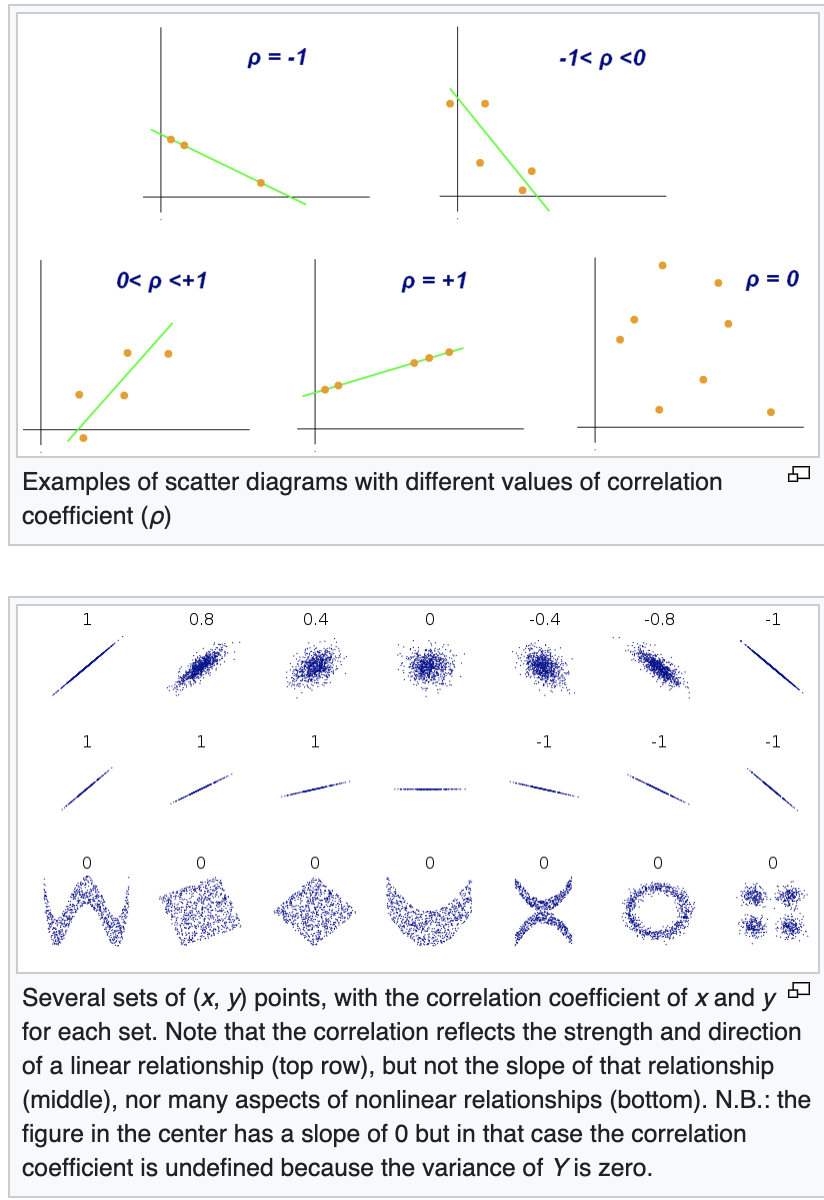
Source: Wikipeida Pearson Correlation Coefficient (opens new window)

Strong correlation is considered : 0.5 - 1.0 or -0.5 to -1.0 can be computed as

df.corr()