Error Function

Trying to reach the bottom of a cliff

What if our function hits a plateau. Where either direction returns the same error. So that is why we want our error function to be continous

Converting predictions using softmax

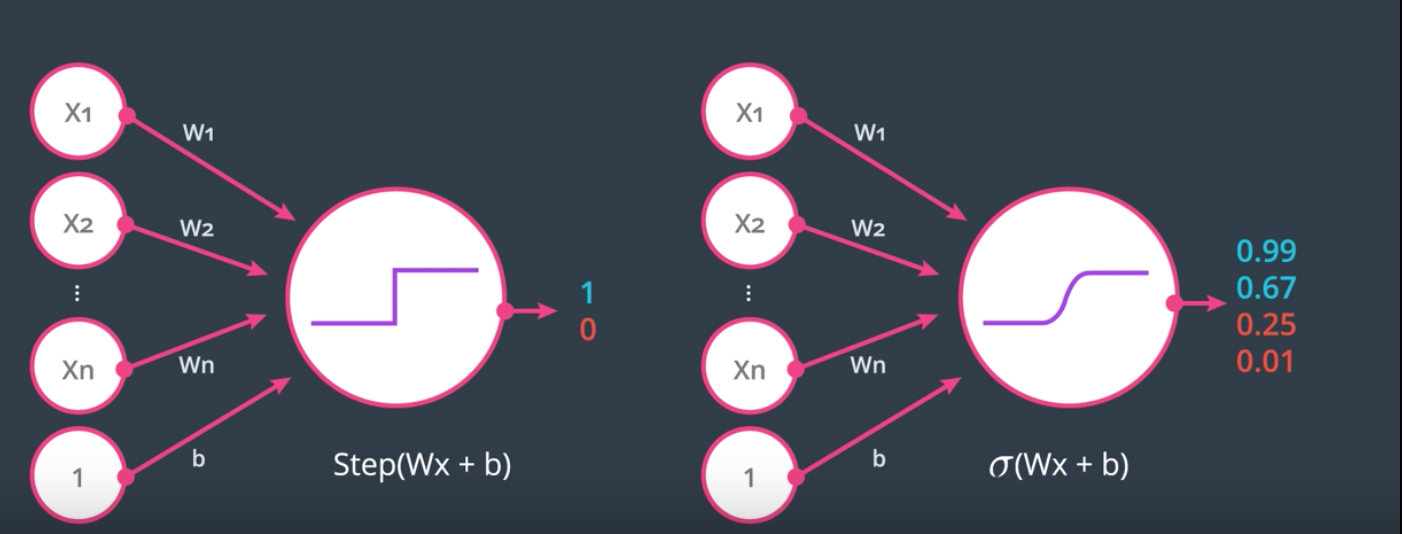
Softmax normalizes output to 0 -1

We use softmax because output could be negative which could lead to division by zero

Sigmoid is a simple case of Softmax

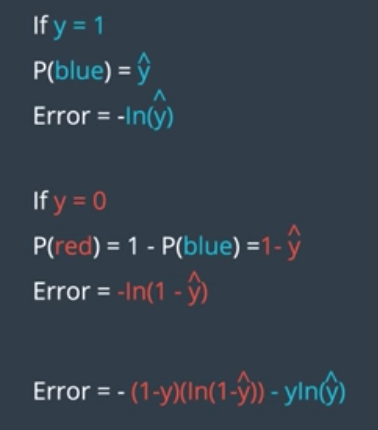
Maximum Likelihood

P(blue) = sigmoid (Wx+b)

The left image is less likely to occur.

Maximizing the porbability is the smae as minimizing the loss.

One problem with multiplying is that the numbers get too small.

The solution is cross entropy.

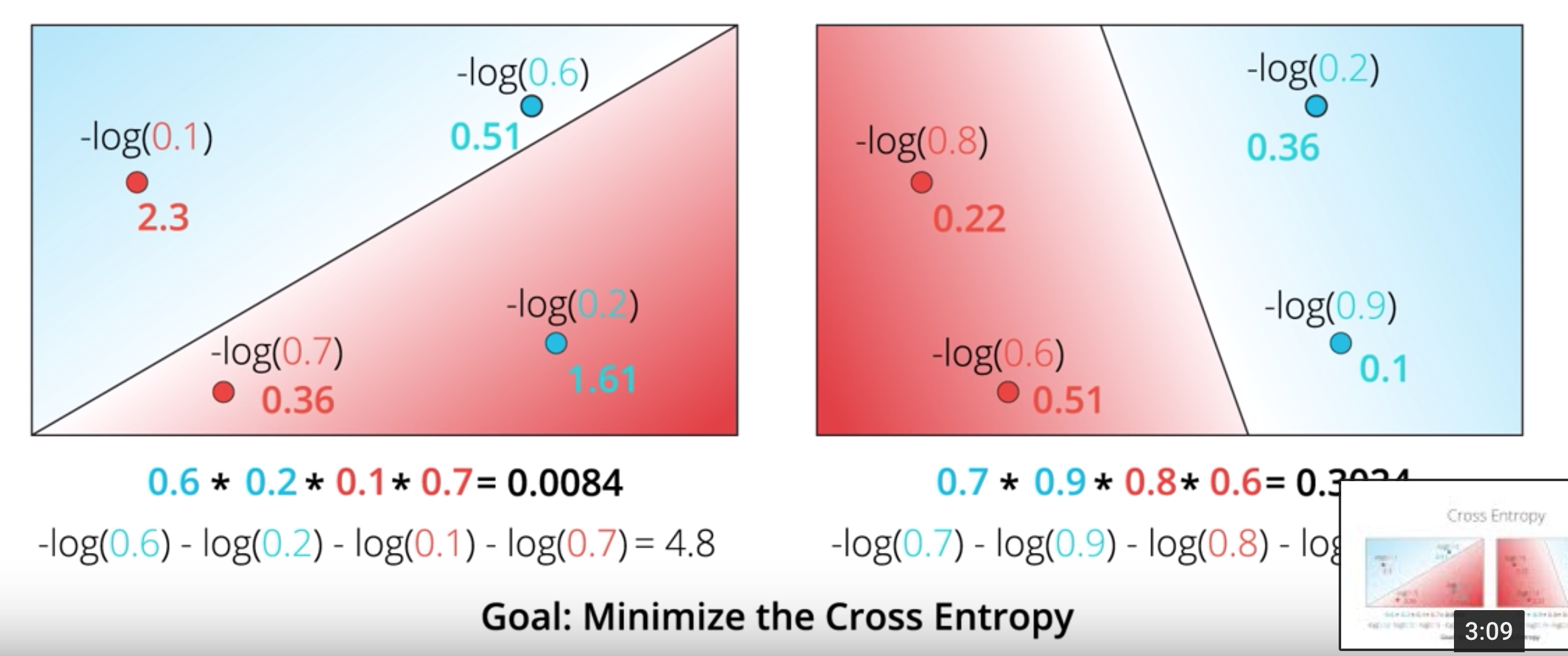
In Cross entropy, we only consider the true class. So y_3=0, so we consider the inverse probability

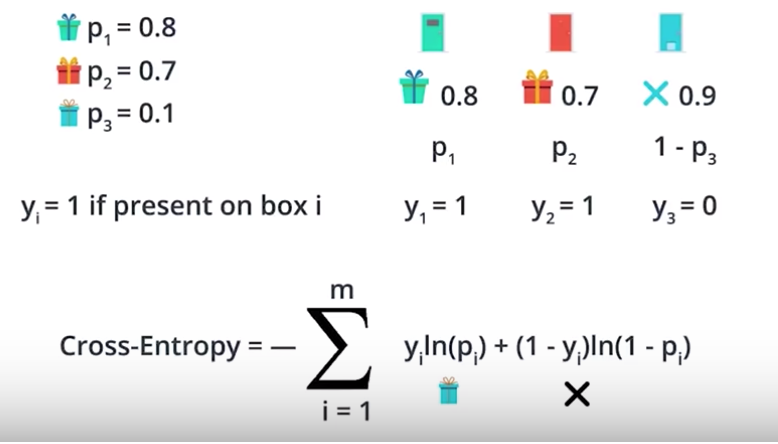
Multi Class Entropy

Is an extension of binary cross entropy. We only consider cases for the actual calss.

m = number of samples n = nuber of classes