U: Documents by topic columns are orthonormal
magnitude is 1; orthogoanl to each other
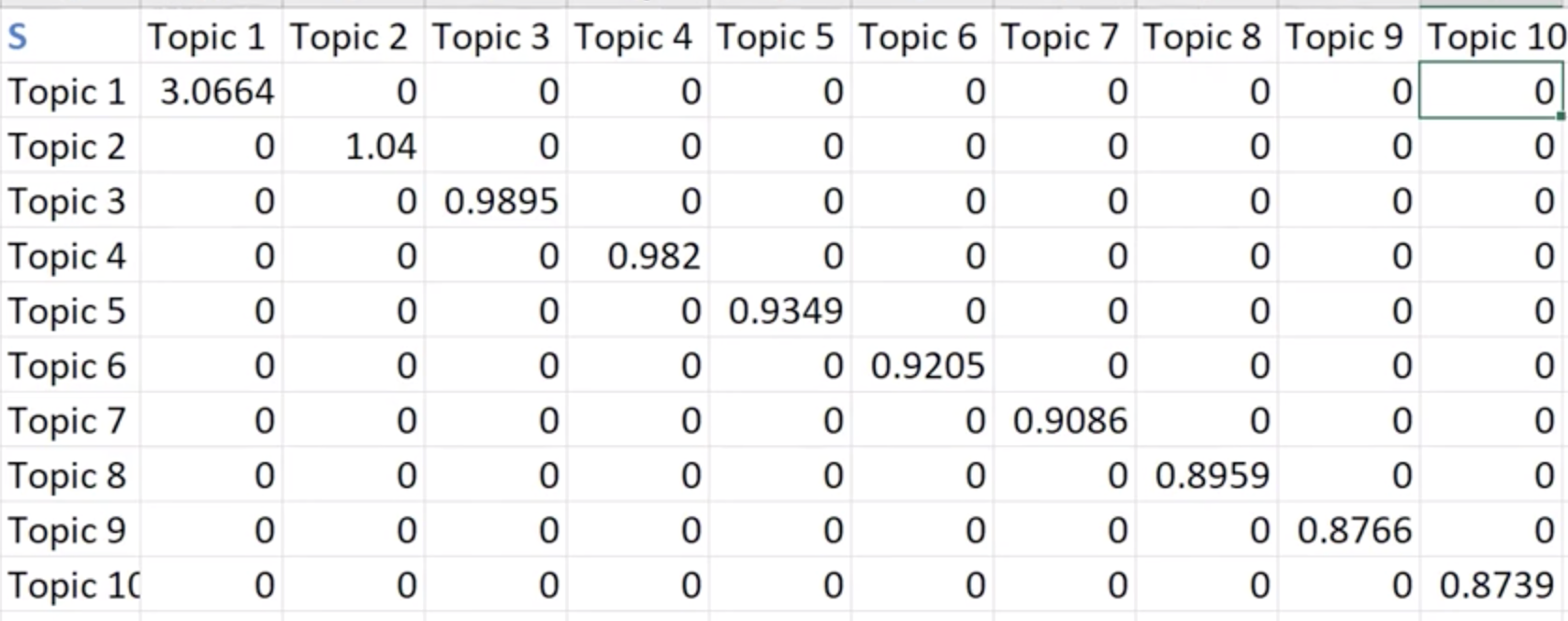
S: Singular Value is diagonal Matrix which shows strength of topic zero values on diagonal
V: relates topic to words
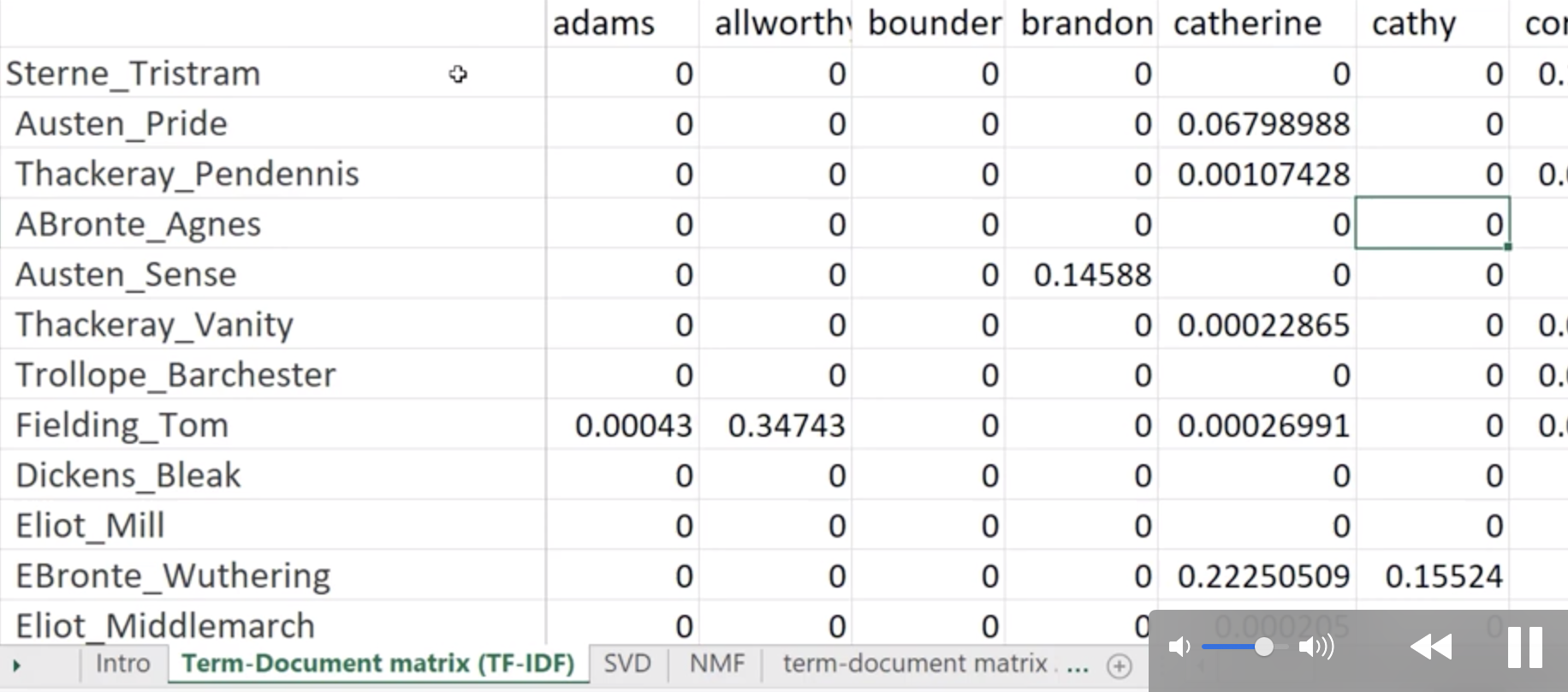
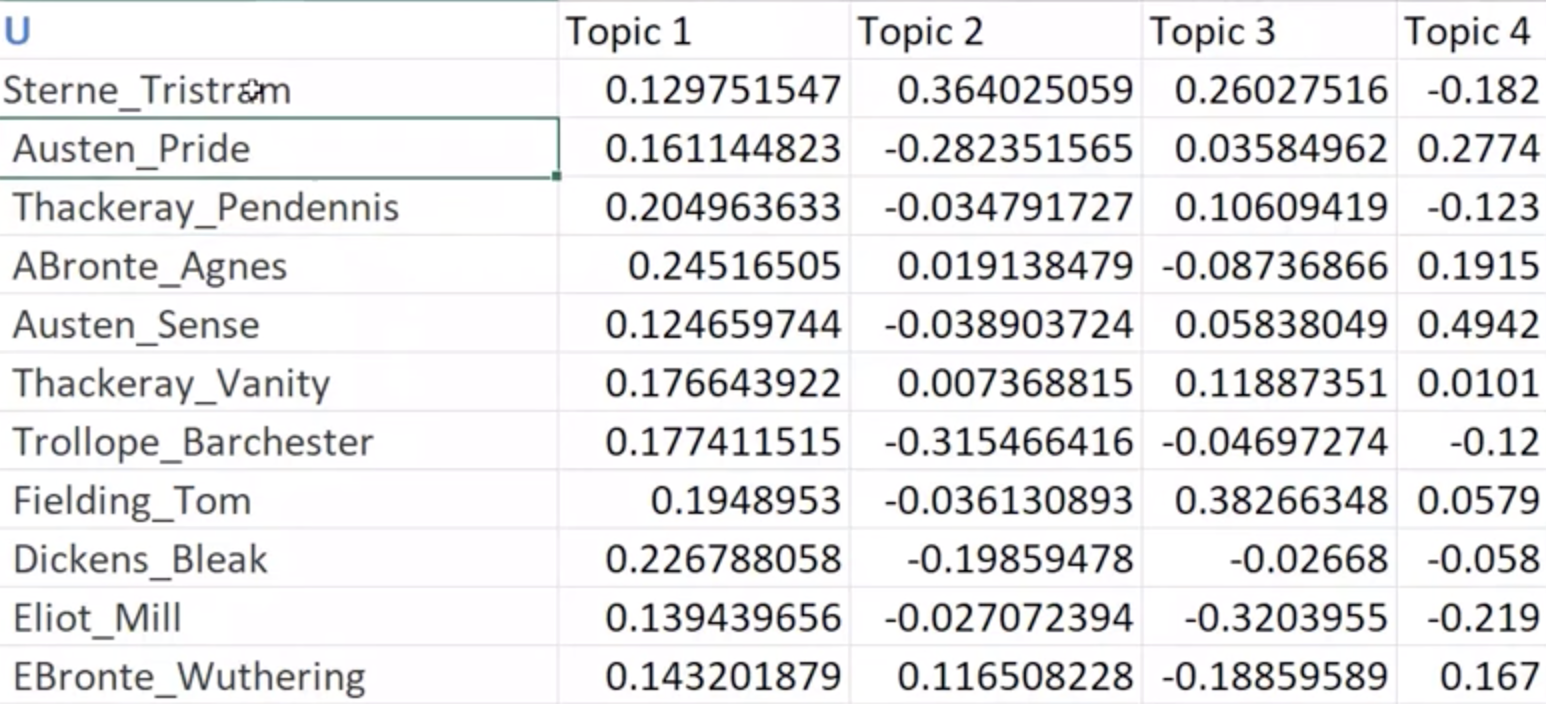
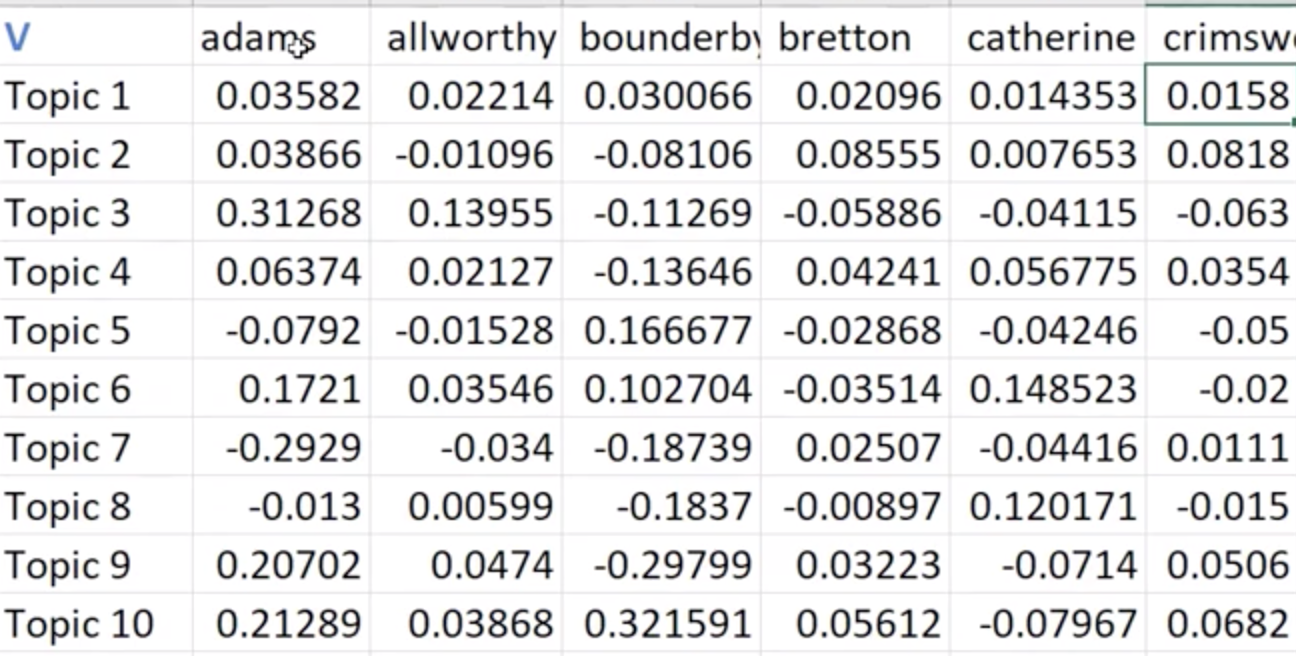
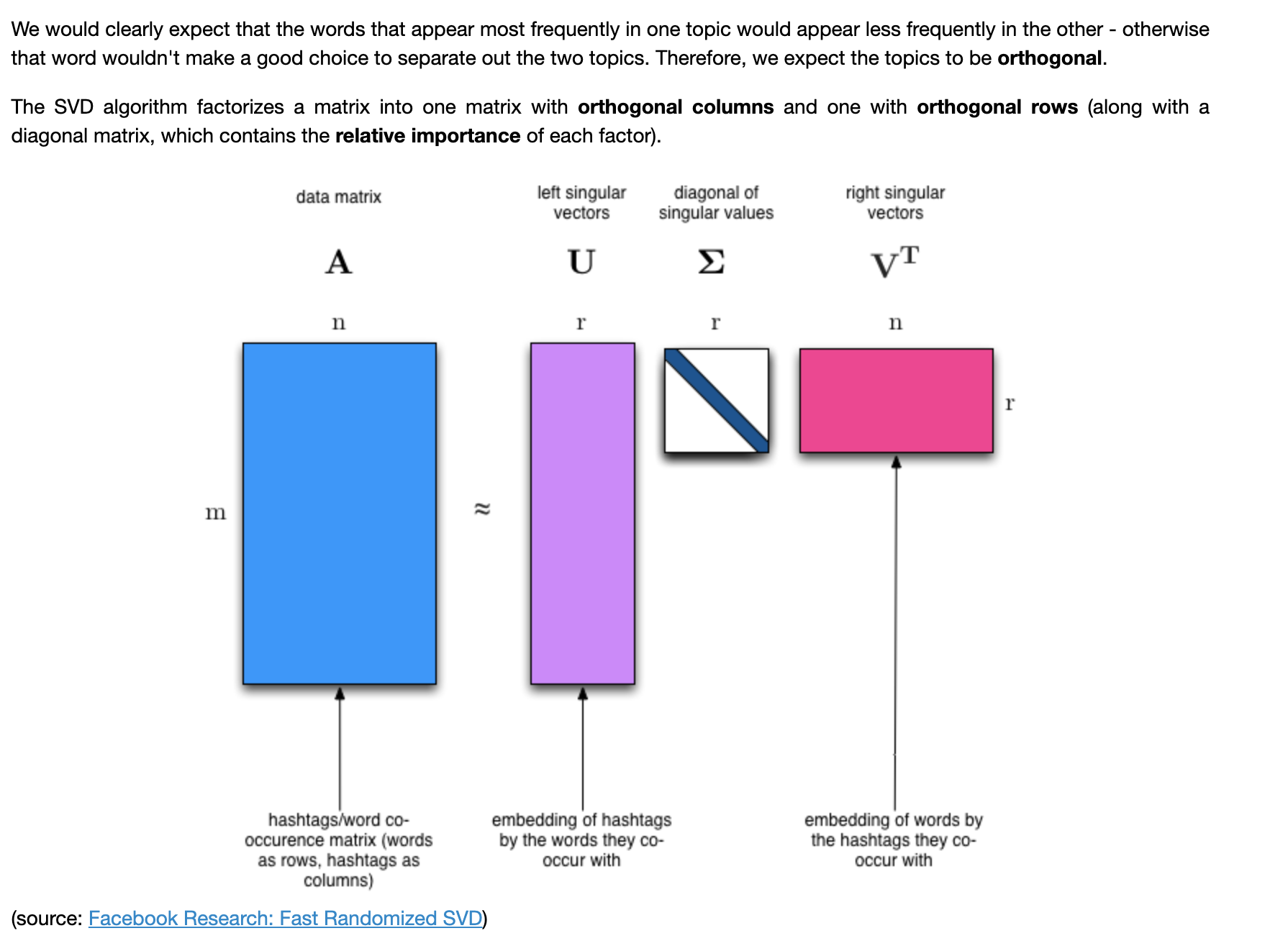
U is orthogonal columns V is orthogonal rows
SVD is an exact decomposition, since the matrices it creates are big enough to fully cover the original matrix. SVD is extremely widely used in linear algebra, and specifically in data science, including:
- semantic analysis
- collaborative filtering/recommendations (winning entry for Netflix Prize)
- data compression
- principal component analysis
Latent Semantic Analysis (LSA) uses SVD.
calculating svd
U, s, Vh = linalg.svd(document_matrix, full_matrices=False)
print(U.shape, s.shape, Vh.shape)
(2034, 2034) (2034,) (2034, 26576)
verify matrix
np.diag converts a vector to a diagonal matirx
reconstructed_matrix = U @ np.diag(s) @ Vh np.allclose(reconstructed_matrix, document_matrix)
We see that the Singular Values are reducing drastically.
Postion 1 is 400 but position 25 is like 10.
Singular Values shows strength of topic.
